Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có:
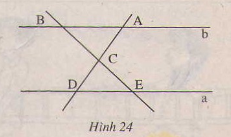
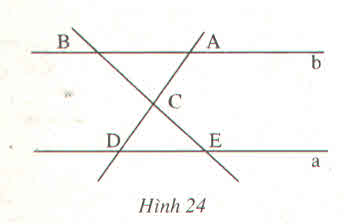
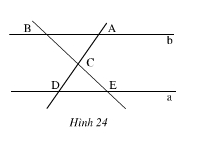
^ECD = ^ACB (2 góc đối đỉnh).
Vì a // b nên:
^ABC = ^CED và ^CDE = BAC (2 góc so le trong)
Vậy các cặp góc bằng nhau của 2 tam giác CAB và CDE là: ^ACB = ^ECD; ^BAC = ^CDE; ^ABC = ^CED.


BAC = DCE (đối đỉnh)
CAB = CDE (so le trong)
ABC = CED (so le trong)

a) Ta có: xy//BC
\(\Rightarrow\widehat{A_1}=\widehat{B}\);\(\widehat{A_2}=\widehat{C}\)
b) Vì \(\widehat{A_1}=\widehat{B}\);\(\widehat{A_2}=\widehat{C}\)
=>\(\widehat{A}+\widehat{B}+\widehat{C}=\widehat{A}+\widehat{A_1}+\widehat{A_2}=180^o\)
Chúc bạn học tốt!
Hình bạn Nguyễn Gia Triệu vẽ rồi nha bạn Trần Thị Thu Huyền
a, Các cặp góc bằng nhau:
\(\widehat{A_1}\)và \(\widehat{B}\); \(\widehat{A_2}\)và \(_{\widehat{C}}\)
b, Ta có:
\(\widehat{A_1=\widehat{B};\widehat{A_2}=\widehat{C}}\)
\(\Rightarrow\widehat{A}+\widehat{B}+\widehat{C}=\widehat{A}+\widehat{A_1+\widehat{A_2}=180^o}\)( theo định lý Py-ta-go về tổng ba cạnh tam giác )




Góc ACB= góc DCE
Góc CAB= góc CDE
Góc CBA= góc CED
góc CAB = góc CDE
góc CBA = góc CED
góc ACB = góc DCE
chúc bạn học tốt