Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Gọi H là chân đường vuông góc kẻ từ A xuống CD
Theo đề bài, ta có: AH=3(cm)
Xét hình bình hành ABCD có AH là đường cao ứng với cạnh CD(gt)
nên \(S_{ABCD}=AH\cdot CD=4\cdot3=12\left(cm^2\right)\)

a, \(S_{ABCD}\) = AH.CD
= 3.4
= 12 (\(cm^2\))
b, Ta có M là trung điểm AB
⇒ AM = \(\dfrac{AB}{2}\) = \(\dfrac{4}{2}\) = 2 (cm)
\(S_{ADM}\) = \(\dfrac{AH.AM}{2}\)
= \(\dfrac{3.2}{2}\)
= 3 (\(cm^2\))
c, Gọi O là trung điểm
c, Gọi O là trung điểm ND
Từ O kẻ OP // CD
Xét ΔNDC có: NO = OD
OP // CD
⇒ OP là đường trung bình ΔNDC
⇒ OP = \(\dfrac{1}{2}DC\) mà DC = 4 cm
⇒ OP = 2 cm
Xét ΔAMN và ΔPON có:
Góc BAC = góc APO
Góc MOP = góc AMD
AM = ON
⇒ ΔAMN = ΔPON (g.c.g)
⇒ NM = ON mà ON = \(\dfrac{1}{2}DM\)
⇒ DN = 2MN

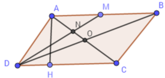
Tứ giác ABCD là hình bình hành nên AC và BD cắt nhau tại trung điểm O của mỗi đường.
Xét tam giác ABD ta có: AO và DM là hai đường trung tuyến của tam giác.
Mà AO ∩ DM = {N} => N là trọng tâm tam giác ADB.
=> AN = 2 3 DM (tính chất đường trung tuyến của tam giác)
Suy ra NM = D M 3
+) Hai tam giác AMN và ADM có cùng đường cao hạ từ A
nên S A M N S A D M = M N D M = 1 3
Mà theo câu trước SADM = 3 cm2
=> SAMN = 1 3 SADM = .3 = 1(cm2)
Đáp án cần chọn là: D

Giải thích các bước giải:
Gọi AH là đg cao từ A xuống cạnh CD
a, diện h hbh=AHxCD=12.16=192
b,M trung điểm AB nên AM=16:2=8cm
vì ABCD là hbh nên đường cao từ D xuống AB= AH=12cm
do đó diện tích tam giác ADM=12x8:2=48
c, Xét tam giác ANM và CND
vì AM//CD nên CDAM=DNMN=12CDAM=DNMN=12 suy ra DN=2NM
d, vì DN=2NM nên chiều cao từ D xuống AM = 3 từ N xuống AM=> chiều cao từ N xuống AM=12:3=4cm
suy ra diện tích AMN=AMx4:2=16
aii giúp mình với