K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
CM
24 tháng 2 2019
Ta có y’=3x2-6x-m
Để đồ thị hàm số đã cho có hai điểm cực trị khi phương trình y’=0 có hai nghiệm phân biệt ⇔ ∆ ' = 9 + 3 m > 0 ⇔ m > - 3
Ta có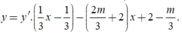 
đường thẳng đi qua hai điểm cực trị Avà B là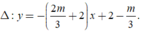 
Đường thẳng d; x+4y-5=0 có một VTPT là n d → = ( 1 ; 4 ) .
Đường thẳng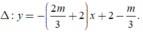 
có một VTCP là
n
∆
→
=
(
2
m
3
+
2
;
1
)
Ycbt suy ra:
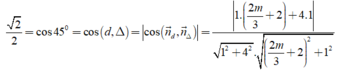
Suy ra
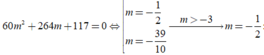thỏa mãn
Chọn A.
\(y'=3x^2-6x-m\)
Hàm số có CĐ, CT khi \(y'=0\) có 2 nghiệm pb
\(\Rightarrow\Delta'=9+3m>0\Rightarrow m>-3\)
Tiến hành chia y cho y' và lấy phần dư ta được phương trình đường thẳng qua CĐ, CT có dạng:
\(y=-\left(\dfrac{2m}{3}+2\right)x-\dfrac{m}{3}+2\)
Do đường thẳng tạo với 2 trục 1 tam giác vuông cân nên có hệ số góc bằng 1 hoặc -1
\(\Rightarrow\left[{}\begin{matrix}-\left(\dfrac{2m}{3}+2\right)=1\\-\left(\dfrac{2m}{3}+2\right)=-1\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}m=-\dfrac{9}{2}< -3\left(loại\right)\\m=-\dfrac{3}{2}\end{matrix}\right.\)