BT
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
14 tháng 6 2023
TH1: x>=3 hoặc x<=1
y=x^2-4x+3+4x+3=x^2+6
y'=2x
x>=3 hoặc 0<=x<=1 thì y'>=0
=>Đồng biến
Khi x<0 thì y'<0
=>Nghịch biến
TH2: 1<x<3
y=-x^2+4x-3+4x+3=-x^2+8x
y'=-2x+8
y'>0
=>x<4
mà 1<x<3
nên 1<x<3
=>Hàm số nghịch biến
CH
1
NV
Nguyễn Việt Lâm
Giáo viên
18 tháng 8 2021
TXĐ: \(D=R\)
\(y'=\dfrac{-5x+8}{2\sqrt{\left(x^2-x+3\right)^3}}=0\Rightarrow x=\dfrac{8}{5}\)
Dấu của y' trên trục số:
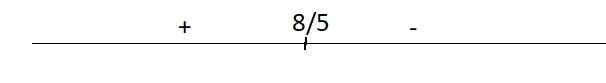
Từ đây ta thấy hàm đồng biến trên \(\left(-\infty;\dfrac{8}{5}\right)\) và nghịch biến trên \(\left(\dfrac{8}{5};+\infty\right)\)
NT
2
7 tháng 7 2023
TXĐ: D=(\(-\infty;2\)]
\(y'=1+2.\dfrac{-1}{2\sqrt{2-x}}\)\(=1-\dfrac{1}{\sqrt{2-x}}\)
Ta có bảng biến thiên sau:
| x | \(-\infty\) 1 2 |
| y' | + 0 - || |
Vậy hàm số đồng biến trên khoảng \(\left(-\infty;1\right)\) và nghịch biến trên khoảng \(\left(1;2\right)\)
MN
Minh Nguyen
Admin
29 tháng 8
Để xác định tính đơn điệu của hàm số \(y = x + 3 + 2\sqrt{2-x}\), ta cần tìm đạo hàm của hàm số này. Đạo hàm của hàm số y theo x là: \[y' = 1 - \frac{2}{\sqrt{2-x}}\] Để xác định tính đơn điệu của hàm số, ta cần xem xét dấu của đạo hàm trên mỗi khoảng xác định của hàm số. - Khi \(2-x > 0\), tức là \(x < 2\), ta có: \[y' = 1 - \frac{2}{\sqrt{2-x}} > 0\] Vậy hàm số tăng trên khoảng \((-\infty, 2)\). - Khi \(2-x < 0\), tức là \(x > 2\), ta có: \[y' = 1 - \frac{2}{\sqrt{2-x}} < 0\] Vậy hàm số giảm trên khoảng \((2, +\infty)\). Vậy, hàm số \(y = x + 3 + 2\sqrt{2-x}\) tăng trên khoảng \((-\infty, 2)\) và giảm trên khoảng \((2, +\infty)\).
TN
1
HN
20 tháng 10 2021
Tập xác định: D=\(\left[-2\sqrt{2};2\sqrt{2}\right]\).
\(y'=1-\dfrac{x}{\sqrt{8-x^2}}\) = 0 \(\Rightarrow\) x=2.
Bảng biến thiên:
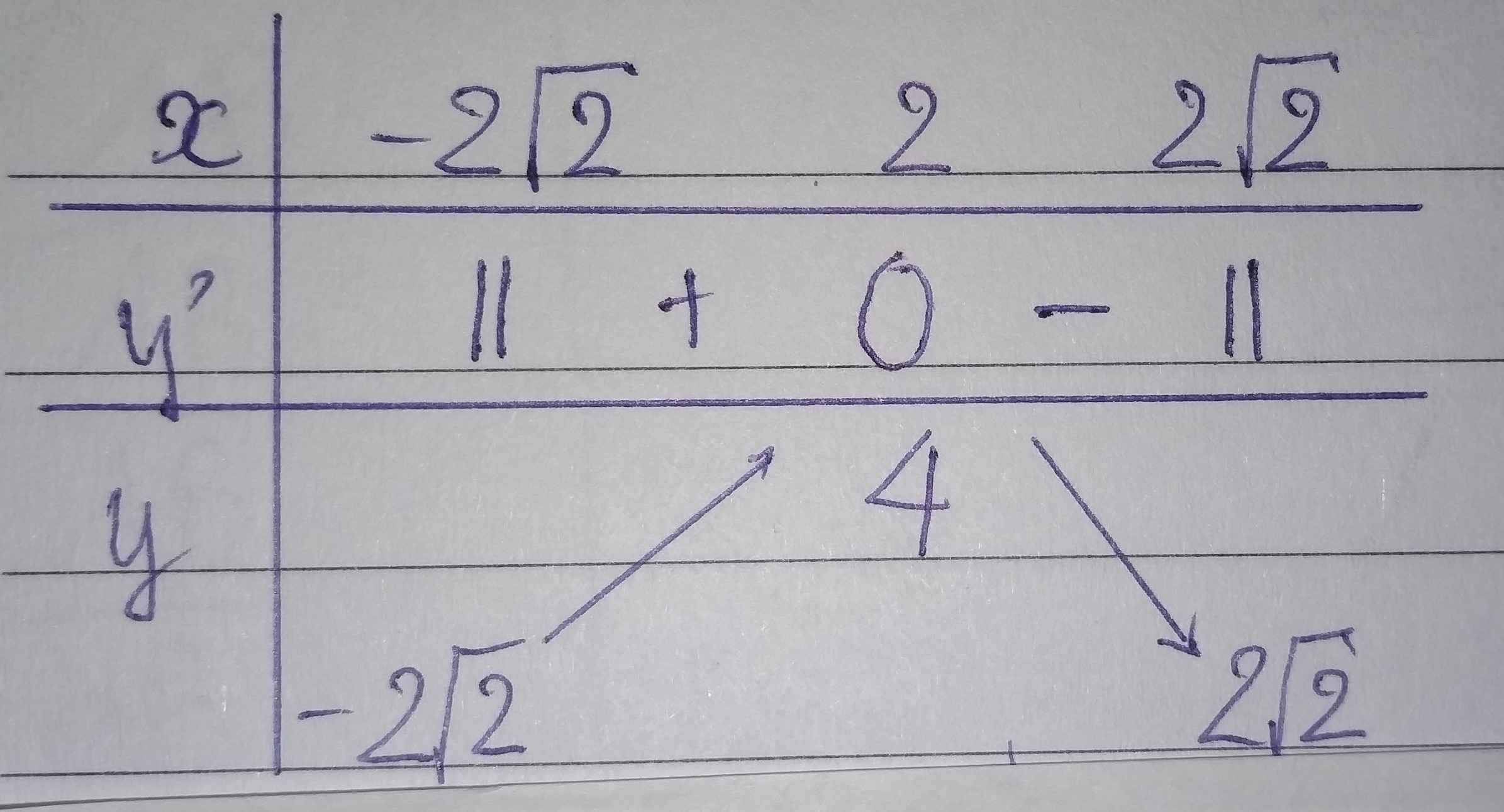
Vậy hàm số đã cho đồng biến trên khoảng (\(-2\sqrt{2}\);2), nghịch biến trên khoảng (2;\(2\sqrt{2}\)) và yCĐ=4 (tại x=2).
Tham khảo: Đồ thị:
LK
1
AH
Akai Haruma
Giáo viên
9 tháng 6 2021
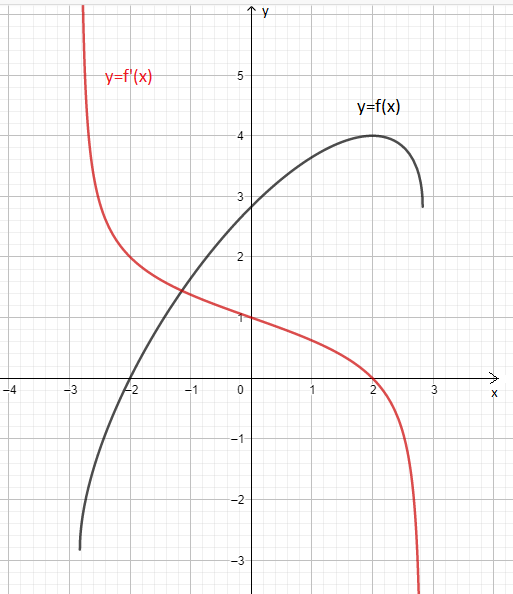
Lời giải:
Với $x\in (5;+\infty)\cup (-\infty;2)$ thì:
$y=x^2+x^2-7x+10=2x^2-7x+10$
$y'=4x-7=0\Leftrightarrow x=\frac{7}{4}$ (không nằm trong khoảng đang xét)
Với $x\in [2;5]$ thì:
$y=x^2-(x^2-7x+10)=7x-10$
$y'=7>0$
Lập BBT ta thấy:
Hàm $y$ đồng biến trên trên $(2;+\infty)$ và nghịch biến trên $(-\infty;2)$
CM
31 tháng 12 2017
- Điều kiện đồng biến, nghịch biến của hàm số:
Cho hàm số y = f(x) có đạo hàm trên khoảng K.
+ f(x) đồng biến (tăng) trên K nếu f’(x) > 0 với ∀ x ∈ K.
+ f(x) nghịch biến (giảm) trên K nếu f’(x) < 0 với ∀ x ∈ K.
- Xét hàm số
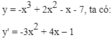
+ Hàm số đồng biến
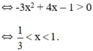
+ Hàm số nghịch biến
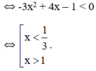
Vậy hàm số đồng biến trên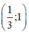 
nghịch biến trên các khoảng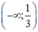 
và (1; +∞)
- Xét hàm số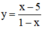 
Ta có: D = R \ {1}
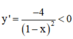∀ x ∈ D.
⇒ Hàm số nghịch biến trên từng khoảng (-∞; 1) và (1; +∞).
PT
1
CM
28 tháng 3 2019
Tập xác định: D = R \ {1}
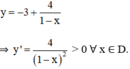
y' không xác định tại x = 1
Bảng biến thiên:
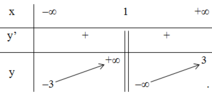
Vậy hàm số đồng biến trên các khoảng (-∞; 1) và (1; +∞)
guaur