Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn C.
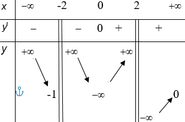
Phương pháp: Dựa vào bảng biến thiên để xác định tiệm cận, cực trị, giá trị lớn nhất, giá trị nhỏ nhất.
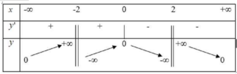
Cách giải: Dựa vào bảng biến thiên dễ thấy đồ thị hàm số có tiệm cận ngang y = 0 và hai tiệm cận đứng x = 2, x = -2. Vậy (I) sai và (IV) đúng.


Đáp án C
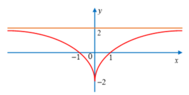
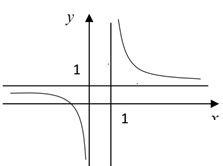
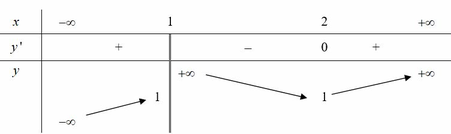
Các đường tiệm cận đứng là x = 1 ; x = − 1.
Tiệm cận ngang là
y
=
−
2
Vậy có tất cả 3 đường tiệm cận

Chọn C
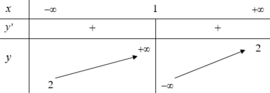
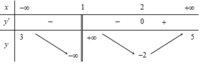
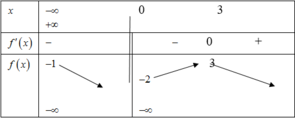
Từ bảng biến thiên ta thấy l i m x → + ∞ y = 5 ; l i m x → ∞ y = 3 đồ thị hàm số có hai đường tiệm cận ngang là y=5 và y=3. Và l i m x → 1 - y = - ∞ ⇒ x = 1 là đường tiệm cận đứng của đồ thị hàm số.
Vậy đồ thị hàm số có tất cả là ba đường tiệm cận

Đáp án là D
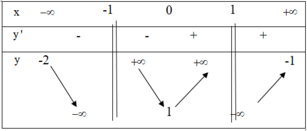
Từ BBT ta có
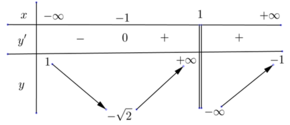
lim x → + ∞ y = − 1 ; lim x → − ∞ y = 1 do đó đồ thị hàm số có hai đường tiệm cận ngang là
y = 1; y =−1.
lim x → 1 − y = + ∞ ; lim x → 1 − y = − ∞ do đó đồ thị hàm số có một đường tiệm cận đứng là x =1. Vậy tổng số có 3 đường tiệm cận




Đáp án D.
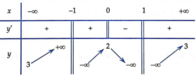
Quan sát bảng biến thiên, ta thấy:
lim x → − 1 − y = + ∞ ; lim x → − 1 + y = − ∞ lim x → 1 − y = − ∞ ; lim x → 1 + y = − ∞ → Đồ thị hàm số có hai đường tiệm cận đứng là x = − 1 và x = 1 . A đúng.
lim x → − ∞ y = 3 ; lim x → + ∞ y = 3 → Đồ thị hàm số có tiệm cận ngang là đường thẳng . B đúng.
Hàm số không có đạo hàm tại điểm , tuy nhiên vẫn đạt giá trị cực đại y=2 tại x=0 . C đúng.
Hàm số không đạt cực trị tại điểm x=1 . D sai.
Cách 1: Tư duy tự luận
Do π > 1 nên π a > π = π 1 ⇔ a > 1 . Vậy A đúng.
Do a > 1 nên a 5 < a 3 ⇔ 5 < 3 (hiển nhiên). Vậy B đúng.
Do e > 1 nên e a > 1 ⇔ e 0 ⇔ a > 0 . Vậy C đúng.
Do a > 1 nên a − 3 > a 2 ⇔ − 3 > 2 (vô lý). Vậy D sai.
Cách 2: Sử dụng máy tính cầm tay
Như vậy nếu a > 1 thì a − 3 < a 2 . Đáp án D sai.