Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
+ Phương trình hoành độ giao điểm: ![]()
+ Điều kiện để d cắt tại hai điểm phân biệt là ![]() .
.
+ Trung điểm của MN là I.
+ Theo công thức đường trung tuyến 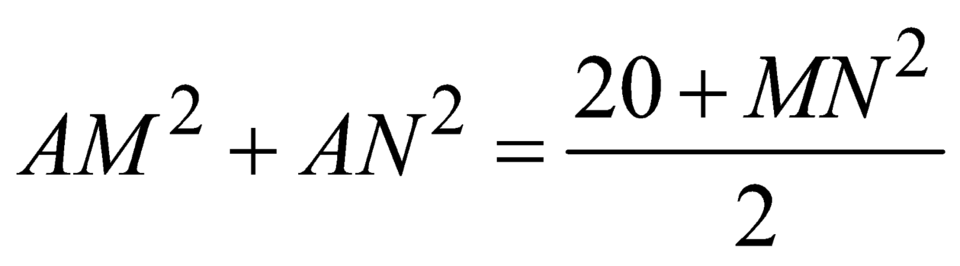 .
.
![]() nhỏ nhất khi
nhỏ nhất khi ![]() nhỏ nhất.
nhỏ nhất.
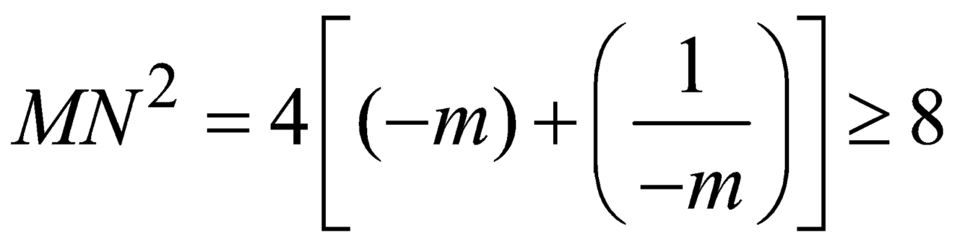 , dấu bằng xảy ra khi
, dấu bằng xảy ra khi ![]()

Chọn C.
Phương pháp
Xét phương trình hoành độ giao điểm.
Đường thẳng cắt đồ thị (C) tại hai điểm phân biệt nếu phương trình hoành độ giao điểm có hai nghiệm phân biệt.
Cách giải:
ĐKXĐ: x ≠ 1
Xét phương trình hoành độ giao điểm x - 1 x + 1 = -x + m (*)
Với x ≠ -1 thì (*) ⇔ x - 1 = (x+1)(-x+m)
![]()
![]()
Đường thẳng y = -x + m cắt đồ thị tại hai điểm phân biệt ⇔ phương trình (**) có hai nghiệm phân biệt khác -1.
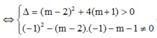
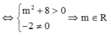
Vậy m ∈ ℝ

Đáp án A
Phương trình hoành độ gioa điểm của d và (C) là
![]()
Suy ra ![]() suy ra
suy ra ![]() Dễ dàng tính được
Dễ dàng tính được ![]()

Đáp án B
Phương trình hoành độ giao điểm hai đồ thị hàm số là:

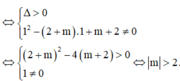

Chọn C.
Phương trình hoành độ giao điểm của đồ thị (C) và đường thẳng d
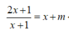
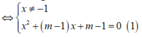
Khi đó d cắt (C) tại hai điểm phân biệt A, B khi và chỉ khi phương trình (1) có hai nghiệm phân biệt khác -1
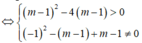
![]()
Ta có
![]()
![]()
![]()
Và 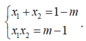
Từ đây ta có
![]()
![]()
![]()
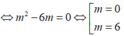 ( thỏa mãn *)
( thỏa mãn *)
Vậy chọn m = 0 hoặc m = 6

Ta có 
Để đồ thị hàm số có hai điểm cực trị khi m khác 0.
Khi đó gọi A( 0 ; -3m-1) và B( 2m ; 4m3-3m-1) là hai điểm cực trị của đồ thị hàm số.
Suy ra trung điểm của AB là điểm I ( m ; 2m3-3m-1) và A B → = ( 2 m ; 4 m 3 ) = 2 m ( 1 ; 2 m 2 )
Đường thẳng d có một vectơ chỉ phương là u → = ( 8 ; - 1 ) .
Ycbt 
Chọn D.

Đáp án C
Phương trình hoành độ giao điểm của (C) và d là:
![]() (*)
(*)
![]()
(C) cắt d tại hai điểm phân biệt ![]() có hai nghiệm phân biệt x1, x2
có hai nghiệm phân biệt x1, x2
![]()
![]()
Gọi ![]() và
và ![]() là các giao điểm của (C) và d với
là các giao điểm của (C) và d với 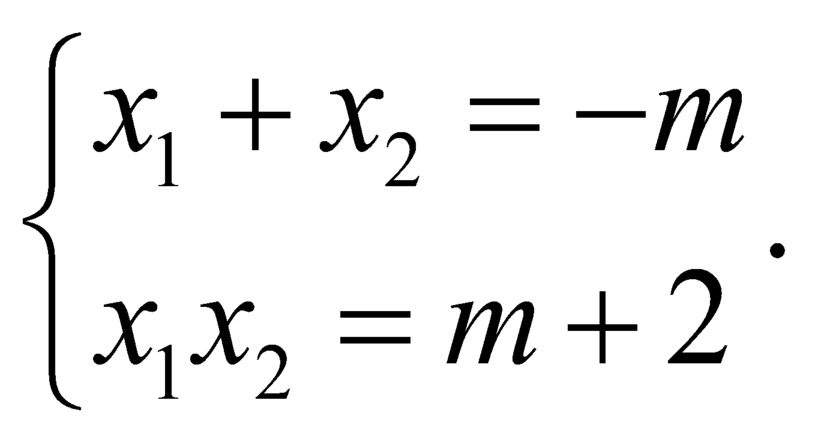
Khi đó
![]()
![]()
![]()
![]()
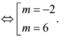
Ngoài ra, ta có thể kiểm tra sau khi có ![]() Khi đó, ta loại các phương án m = 1; m = 5
Khi đó, ta loại các phương án m = 1; m = 5
Thử một phương án m = -2, ta được phương trình:
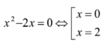
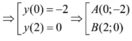
![]()

Lời giải:
PT hoành độ giao điểm:
$\frac{2mx-3}{x-1}=x+1$
$\Leftrightarrow x^2-2mx+2=0(*)$
Để 2 ĐTHS cắt nhau tại 2 điểm $A,B$ thì PT $(*)$ có 2 nghiệm phân biệt $x_A,x_B$
$\Leftrightarrow \Delta'=m^2-2>0$
Áp dụng định lý Viet: $x_A+x_B=2m$
$A,B$ đối xứng với nhau qua đường thẳng $d_1$ thì $d_1$ đi qua trung điểm của $AB$
$\Leftrightarrow (\frac{x_A+x_B}{2}, \frac{y_A+y_B}{2})\in d_1$
$\Leftrightarrow \frac{y_A+y_B}{2}=-\frac{x_A+x_B}{2}+7$
$\Leftrightarrow \frac{x_A+1+x_B+1}{2}=-\frac{x_A+x_B}{2}+7$
$\Leftrightarrow x_A+x_B=6$
$\Leftrightarrow 2m=6\Leftrightarrow m=3$ (thỏa mãn)