Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

b: Vì \(a=-\dfrac{5}{9}< 0\) nên hàm số luôn nghịch biến trên R

\(\dfrac{f\left(x_1\right)-f\left(x_2\right)}{x_1-x_2}=\dfrac{3x_1-2-3x_2+2}{x_1-x_2}=3\)
Vậy: Hàm số đồng biến trên R

`a=m^2+m+1=m^2+2.m. 1/2 + (1/2)^2 + 3/4= (m+1/2)^2 + 3/4 >0 forall m`
`=> a>0 =>` Hàm số luôn đồng biến trên `RR`.
Để hàm số trên đồng biến khi \(m^2+m+1=m^2+m+\dfrac{1}{4}+\dfrac{3}{4}=\left(m+\dfrac{1}{2}\right)^2+\dfrac{3}{4}>0\)
Vậy hàm số luôn đồng biến trên R

a, Để y = (m - 1)x + 2m - 3 là hàm số bậc nhất thì a \(\ne\) 0 \(\Leftrightarrow\) m - 1 \(\ne\) 0 \(\Leftrightarrow\) m \(\ne\) 1
y = (m - 1)x + 2m - 3 đồng biến trên R \(\Leftrightarrow\) a > 0 \(\Leftrightarrow\) m - 1 > 0 \(\Leftrightarrow\) m > 1
y = (m - 1)x + 2m - 3 nghịch biến trên R \(\Leftrightarrow\) a < 0 \(\Leftrightarrow\) m - 1 < 0 \(\Leftrightarrow\) m < 1
b, f(1) = 2
\(\Leftrightarrow\) (m - 1).1 + 2m - 3 = 2
\(\Leftrightarrow\) m - 1 + 2m - 3 = 2
\(\Leftrightarrow\) m = 2
Với m = 2 ta có:
f(2) = (2 - 1).2 + 2.2 - 3 = 3
Vậy f(2) = 3
c, f(-3) = 0
\(\Leftrightarrow\) (m - 1).0 + 2m - 3 = 0
\(\Leftrightarrow\) 2m = 3
\(\Leftrightarrow\) m = 1,5
Vì m > 1 (1,5 > 1)
\(\Rightarrow\) m - 1 > 0
hay a > 0
Vậy hàm số y = f(x) = (m - 1).x + 2m - 3 đồng biến trên R
Chúc bn học tốt!

a: Hàm số này đồng biến vì \(2-\sqrt{3}>0\)
b: \(f\left(2+\sqrt{3}\right)=4-3-1=0\)
\(f\left(\sqrt{3}\right)=2\sqrt{3}-3-1=2\sqrt{3}-4\)

Gia su \(x_1< x_2\)
\(\Rightarrow x_1-x_2< 0\left(1\right)\)
Ta co:
\(f\left(x_1\right)-f\left(x_2\right)=\left(3m^2-7m+5\right)x_1-2011-\left(3m^2-7m+5\right)x_2+2011=\left(x_1-x_2\right)\left(3m^2-7m+5\right)\)Vi la chung minh dong bien nen xet
\(3m^2-7m+5>0\)
Dat \(g\left(m\right)=3m^2-7m+5\)
Ta lai co:
\(\Delta=\left(-7\right)^2-4.3.5=-11< 0\)
Theo dinh li dau tam thuc bac hai thi \(g\left(m\right)\)cung dau voi he so 3
\(\Rightarrow3m^2-7m+5>0\left(2\right)\left(\forall m\right)\)
Tu \(\left(1\right)\)va \(\left(2\right)\)suy ra;
\(\left(x_1-x_2\right)\left(3m^2-7m+5\right)< 0\)
Ma \(f\left(x_1\right)-f\left(x_2\right)=\left(x_1-x_2\right)\left(3m^2-7m+5\right)\)
\(\Rightarrow f\left(x_1\right)< f\left(x_2\right)\)
Vay ham so \(y=f\left(x\right)=\left(3m^2-7m+5\right)x-2011\)dong bien voi moi m

a) Ta có:
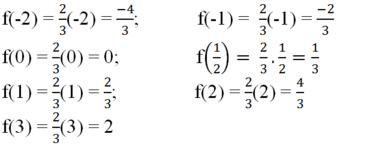
b) Ta có:
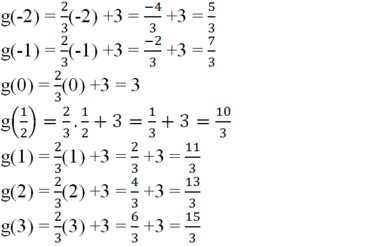
c) Từ kết quả câu a, b ta được bảng sau:

Nhận xét:
- Hai hàm số
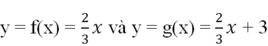
là hai hàm số đồng biến vì khi x tăng thì y cũng nhận được các giá trị tương ứng tăng lên.
- Cùng một giá trị của biến x, giá trị của hàm số y = g(x) luôn luôn lớn hơn giá trị tương ứng của hàm số y = f(x) là 3 đơn vị.
a) \(f\left(0\right)=\dfrac{2}{7}.0-8=-8\)
\(f\left(2\right)=\dfrac{3}{7}.2-8=-\dfrac{50}{7}\)
\(f\left(-1\right)=\dfrac{3}{7}.\left(-1\right)-8=-\dfrac{59}{7}\)
\(f\left(-2\right)=\dfrac{3}{7}.\left(-2\right)-8=-\dfrac{62}{7}\)
b) Với mọi \(x_1,x_2\in R\), ta có
\(x_1>x_2\Leftrightarrow\dfrac{3}{7}x_1>\dfrac{3}{7}x_2\Leftrightarrow\dfrac{3}{7}x_1-8>\dfrac{3}{7}x_2-8\Leftrightarrow f\left(x_1\right)>f\left(x_2\right)\)
\(\Rightarrow\) Hàm số luôn đồng biến trên R
b: Vì \(a=\dfrac{3}{7}>0\) nên hàm số đồng biến trên R