Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
Tiệm cận đứng: d 1 : x = - 1 , tiệm cận ngang d 2 : y = 1 suy ra tâm đối xứng là I ( - 1 ; 1 ) . Phương trình tiếp tuyến tại M a ; a + 2 a + 1 ∈ ( C ) a ≠ - 1 là: y = - 1 ( a + 1 ) 2 x - a + a + 2 a + 1 d
Khi đó d I ; d = - 1 a + 1 2 - 1 - a - 1 + a + 2 a + 1 1 a + 1 4 + 1 = 2 a + 1 1 a + 1 4 + 1 = 2 1 a + 1 2 + a + 1 2 ≤ 2 2 1 a + 1 2 . a + 1 2 . Hay d ≤ 2 2 = 2 .

Chọn C.
Phương pháp: Viết phương trình tiếp tuyến và tính khoảng cách, sau đó sử dụng điều kiện có nghiệm để tìm giá trị lớn nhất.

Tọa độ giao điểm của hai đường tiệm cận của (C) là I(-1;1)
Ta có:


Đáp án A
Ta có: I 3 2 ; 1 2 . PTTT tại điểm M bất kì là: y = − 1 2 x 0 − 3 2 x − x 0 + x 0 − 1 2 x 0 − 3 Δ
Khi đó: d I ; Δ = 1 2 2 x 0 − 3 + x 0 − 1 2 x 0 − 3 − 1 2 1 2 x 0 − 3 + 1 = 1 1 2 x 0 − 3 2 + 2 x 0 − 2 2 ≤ 1 2

Đáp án C.
Ta có I 2 ; 1 .
Tiếp tuyến với C tại điểm M x 0 ; x 0 + 2 x 0 − 2 là d : y = − 4 x 0 − 2 2 x − x 0 + x 0 + 2 x 0 − 2
Tọa độ A là nghiệm của hệ
y = − 4 x 0 − 2 2 x − x 0 + x 0 + 2 x 0 − 2 x = 2 ⇒ y = 4 x 0 − 2 + x 0 + 2 x 0 − 2 ⇒ A 2 ; x 0 + 6 x 0 − 2 ⇒ I A → = 0 ; 8 x 0 − 2
Tọa độ B là nghiệm của hệ
y = − 4 x 0 − 2 2 x − x 0 + x 0 + 2 x 0 − 2 y = 2 ⇒ x 0 − 2 2 = − 4 x − x 0 + x 0 2 − 4 ⇒ B 2 x 0 − 2 ; 1 ⇒ I B → = 2 x 0 − 4 ; 0 Do đó C I A B = π . A B = π I A 2 + I B 2 ≥ π 2 I A . I B
Mà I A . I B = 8 x 0 − 2 . 2 x 0 − 4 = 16 ⇒ C I A B ≥ 4 π 2

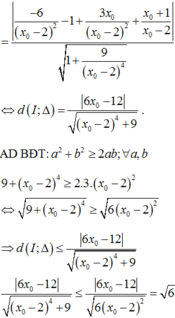

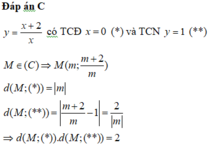


Đáp án D