Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

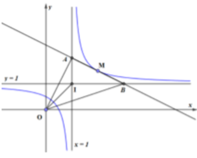
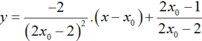
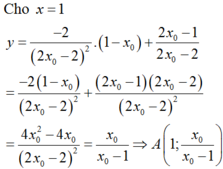
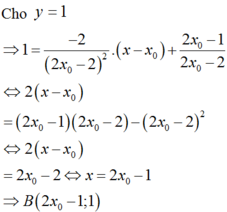
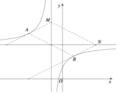
Đồ thị (C) có TCĐ là x = 1 và TCN là y = 1 , giao điểm của 2 đường tiệm cận I 1 ; 1
Ta có:
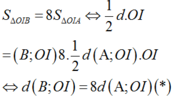
Phương trình đường thẳng OI là:
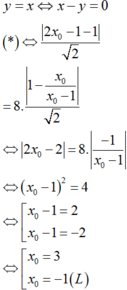
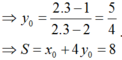
Chọn: A

Chọn đáp án B.

d và (C) cắt nhau tại ba điểm phân biệt

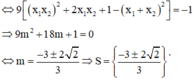
Tổng bình phương các phần tử của S là


Gọi M x 0 ; 3 x 0 - 2 x 0 + 1 ∈ C x 0 ≠ - 1
Tiếp tuyến d với (C) tại M có phương trình: y - 3 x 0 - 2 x 0 + 1 = 5 x 0 + 1 2 x - x 0
Do d cắt tiệm cận đứng, tiệm cận ngang lần lượt tại A, B và ∆ I A B có cos B A I ^ = 5 26 26 nên B A I ^ = 5
Lại có B A I ^ là hệ số góc của tiếp tuyến d mà y ' x 0 = 5 x 0 + 1 2 > 0 nên
5 x 0 + 1 2 = 5 ⇔ x 0 + 1 2 = 1 ⇔ x 0 = 2 x 0 = 1
Vậy có hai tiếp tuyến thỏa mãn yêu cầu bài toán y = 5x - 2; y = 5x + 2
Đáp án C

Giao điểm của hai đường tiệm cận là I ( -1;2 )
y = 2 x - 1 x + 1 ⇒ y ' = 3 x + 1 2 ⇒ PTTT tại M x 0 , y 0 là
( d ) y = 3 x 0 + 1 2 x - x 0 + 2 x 0 - 1 x 0 + 1
Giao của (d) với TCD x = -1 là A - 1 ; 2 x 0 - 4 x 0 - 1 , Giao của (d) với TCD B 2 x 0 + 1 ; 2
A B 2 + I B 2 = 40 ⇔ 2 - 2 x 0 - 4 x 0 - 1 2 + - 2 x 0 - 2 2 = 40
⇔ 36 x 0 + 1 2 + 4 x 0 + 1 2 = 40
x 0 + 1 4 - 10 x 0 + 1 2 + 9 = 0 ⇔ x 0 + 1 2 = 1 x 0 + 1 2 = 9 ⇒ x 0 = 2 x 0 > 0 ⇒ y 0 = - 1 ⇒ x 0 y 0 = 2
Đáp án cần chọn là D



Đáp án C
Phương pháp :
+) Viết phương trình tiếp tuyến của đồ thị hàm số tại điểm có hoành độ m – 2
y = f’(m – 2)(x – m +2)+y(m – 2) (d)
+) Xác định các giao điểm của d và các đường tiệm cận => x2;y1
+) Thay vào phương trình x2 + y1 = –5 giải tìm các giá trị của m.
Cách giải: TXĐ: D = R\ {–2}
Ta có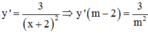
=>Phương trình tiếp tuyến của đồ thị hàm số tại điểm có hoành độ m – 2 là: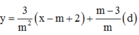
Đồ thị hàm số y = x - 1 x + 2 có đường TCN y = 1và tiệm cậm đứng x = –2