Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Hàm không có tiệm cận đứng khi: \(x^2-\left(2m+3\right)x+2\left(m-1\right)=0\) có nghiệm \(x=2\)
\(\Rightarrow4-2\left(2m+3\right)+2\left(m-1\right)=0\)
\(\Rightarrow m=-2\)

Lời giải:
Theo đề thì cần tìm $m$ để đths đã cho cho TCĐ $x=2$
Điều này xảy ra khi mà $2x+2m=0$ tại $x=2$
$\Leftrightarrow m=-x=-2$
Đáp án B.

Hàm có 2 tiệm cận đứng khi và chỉ khi phương trình: \(x^2+2\left(m-1\right)x+m^2-2=0\) có 2 nghiệm phân biệt khác 1
\(\Leftrightarrow\left\{{}\begin{matrix}1+2\left(m-1\right)+m^2-2\ne0\\\Delta'=\left(m-1\right)^2-\left(m^2-2\right)>0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m^2+2m-3\ne0\\-2m+3>0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m< \dfrac{3}{2}\\m\ne\left\{1;-3\right\}\end{matrix}\right.\)

Chọn D
Đồ thị hàm số
![]()
có đúng hai tiệm cận đứng
⇔ phương trình ![]() có hai nghiệm phân biệt
có hai nghiệm phân biệt
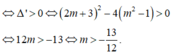

Chọn D
Đồ thị hàm số ![]() có đúng hai tiệm cận đứng
có đúng hai tiệm cận đứng
⇔ phương trình ![]()
có hai nghiệm phân biệt
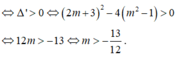

Đề bài sai, do pt \(x^2+3x+4=0\) vô nghiệm nên đồ thị hàm số không có TCĐ nào với mọi m


Ta có:
⇒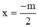 là tiệm cận đứng của đồ thị hàm số.
là tiệm cận đứng của đồ thị hàm số.
+ Tiệm cận đứng đi qua A 1 ; 2
⇔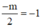
⇔ m = 2.
Vậy với m = 2 thì tiệm cận đứng của đồ thị đi qua A - 1 , 2