Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

3.
\(y'=\dfrac{3m-1}{\left(x+3m\right)^2}\)
Hàm nghịch biến trên khoảng đã cho khi:
\(\left\{{}\begin{matrix}3m-1< 0\\-3m\le6\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}m< \dfrac{1}{3}\\m\ge-2\end{matrix}\right.\)
\(\Rightarrow-2\le m< \dfrac{1}{3}\Rightarrow m=\left\{-2;-1;0\right\}\)
4.
\(y'=\dfrac{3m-2}{\left(x+3m\right)^2}\)
Hàm đồng biến trên khoảng đã cho khi:
\(\left\{{}\begin{matrix}3m-2>0\\-3m\ge-6\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}m>\dfrac{2}{3}\\m\le2\end{matrix}\right.\)
\(\Rightarrow\dfrac{2}{3}< m\le2\Rightarrow m=\left\{1;2\right\}\)

Theo mình:
để hàm số đồng biến, đk cần là y'=0.
a>0 và \(\Delta'< 0\)
nghịch biến thì a<0
vì denta<0 thì hầm số cùng dấu với a
mình giải được câu a với b
câu c có hai cực trị thì a\(\ne\)0, y'=0, denta>0 (để hàm số có hai nghiệm pb)
câu d dùng viet
câu e mình chưa chắc lắm ^^

Để hàm số \(y = (m^2-1)x^3 + (m-1)x^2 - x + 4\) nghịch biến trên khoảng \((-∞;+∞)\), ta cần xác định điều kiện để đạo hàm của hàm số này luôn âm hoặc dương trên khoảng đó. Đạo hàm của hàm số theo x là: \[y' = 3(m^2-1)x^2 + 2(m-1)x - 1\] Để hàm số nghịch biến trên khoảng \((-∞;+∞)\), ta cần giải phương trình \(y' = 0\) và xác định điều kiện để \(y' > 0\) hoặc \(y' < 0\) trên khoảng đó. Giải phương trình \(y' = 0\): \[3(m^2-1)x^2 + 2(m-1)x - 1 = 0\] Điều kiện để hàm số nghịch biến là \(y' > 0\) hoặc \(y' < 0\), ta cần xác định điều kiện của \(m\) sao cho đồng biến hoặc nghịch biến trên khoảng \((-∞;+∞)\). Vậy, số nguyên \(m\) thoả mãn là số nguyên nào?

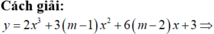
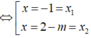

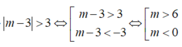




Khi đó y' là hàm số bậc ba. Phương trình y'=0 có ít nhất một nghiệm đơn hoặc bội lẻ và đổi dấu qua nghiệm đó. Do đó mệnh đề (*) sai. Suy ra loại m 2 - 3 m + 2 ≠ 0
Chọn A