Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bạn tham khảo ạ!
Cho hàm số f(x) = \(\dfrac{x+m}{x+1}\) (m là tham số thực). Gọi S là tập hợp tất cả các giá trị của tham số m sao cho \(... - Hoc24
Còn nếu chưa hiểu cách làm thì bạn có thể hỏi anh Lâm hoặc chính người làm bài này :)
Lời giải:
Nếu $m=1$ thì hàm $f(x)=1$ là hàm hằng thì không có cực trị.
Nếu $m\neq 1$;
$f'(x)=\frac{1-m}{(x+1)^2}$. $m>1$ thì hàm nghịch biến trên $[0;1]$, mà $m< 1$ thì hàm số đồng biến trên $[0;1]$
Từ đó suy ra hàm số đạt cực trị tại biên, tức là $(f_{\min}, f_{\max})=(f(1),f(0))=(m, \frac{m+1}{2})$ và hoán vị.
Giờ ta đi giải PT:
$|m|+|\frac{m+1}{2}|=2$
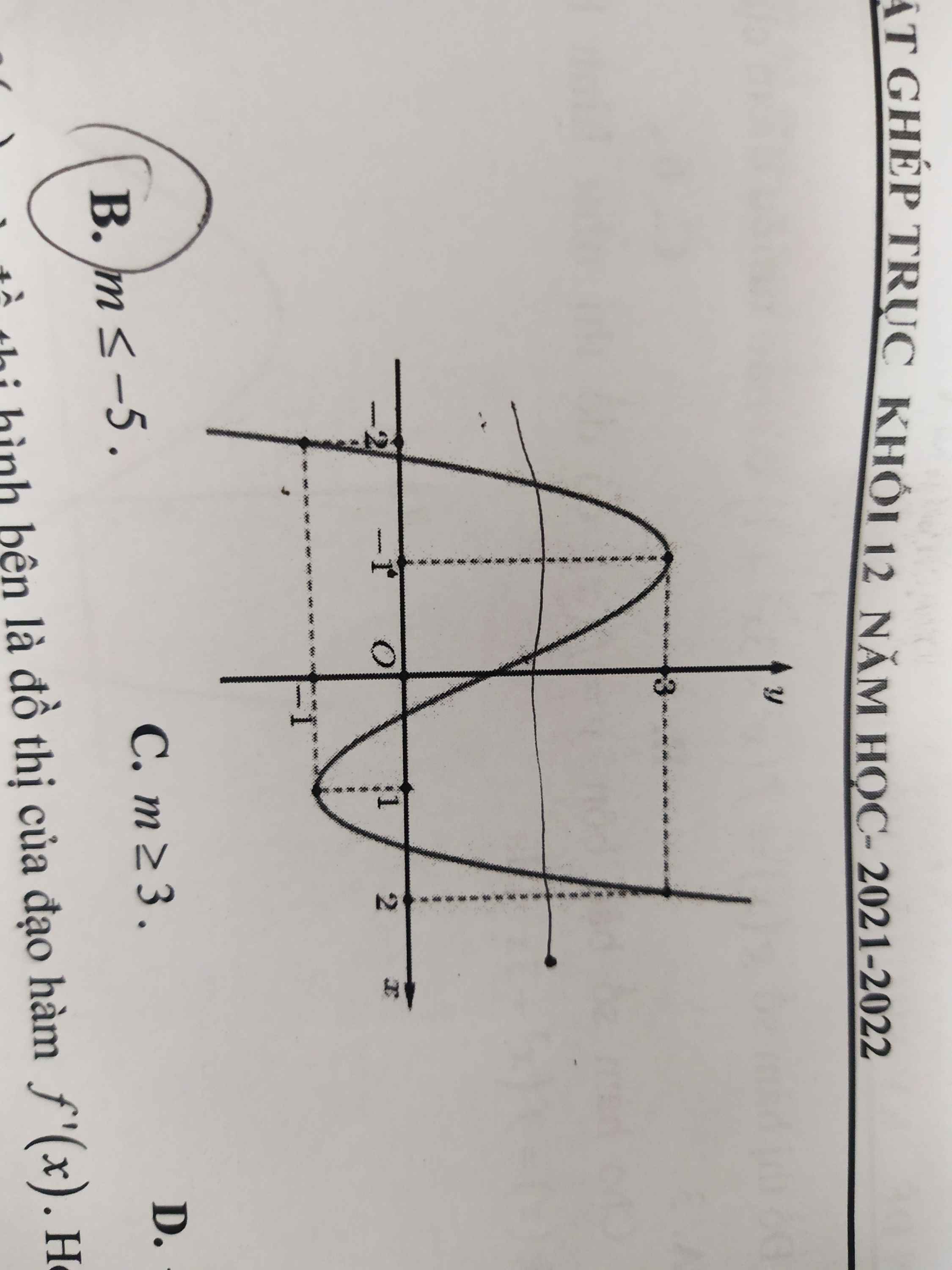
Dễ dàng giải ra $m=1$ hoặc $m=\frac{-5}{3}$
Do đó đáp án là B.

\(g'\left(x\right)=0\Rightarrow x=0\)
Ta thấy \(g\left(x\right)\) đồng biến trên \(\left(0;+\infty\right)\)
\(\Rightarrow g\left(f\left(x\right)\right)\) đồng biến khi \(f\left(x\right)\ge0\)
\(\Rightarrow g\left(f\left(x\right)\right)\) đồng biến trên \(\left(3;+\infty\right)\) khi \(f\left(x\right)\ge0\) ; \(\forall x>3\)
\(\Leftrightarrow x^2-4x\ge-m\) ; \(\forall x>3\)
\(\Leftrightarrow-m\le\min\limits_{x>3}\left(x^2-4x\right)\)
\(\Rightarrow-m\le-3\Rightarrow m\ge3\)