Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Đáp án D
Đồ thị hàm số y = 1 2 x - 3 có hai đường tiệm cận đứng và một đường tiệm cận ngang
Đồ thị hàm số y = x + x 2 + x + 1 x có 1 tiệm cận đứng là x = 0
Mặt khác lim x → + ∞ y = x + x 2 + x + 1 x = lim x → + ∞ x + x + 1 x + 1 x 2 x = 0 nên đồ thị hàm số có 2 tiệm cận ngang
Xét hàm số y = x - 2 x - 1 x 2 - 1 = x - 2 x - 1 x + 2 x - 1 x 2 - 1 = x - 1 x + 2 x - 1 x - 1 x > 1 2 suy ra đồ thị không có tiệm cận đứng. Do đó có 1 mệnh đề đúng
Phương pháp:
Dựa vào các tính chất của đồ thị hàm số mũ và hàm số logarit.
Cách giải:
Cả 4 phát biểu đều đúng
Chọn C
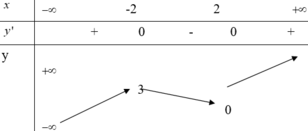
Hàm số xác định 
vì đường thẳng y=0 cắt đồ thị f(x) tại hai điểm có hoành độ x=a<-2; x=2
Ta có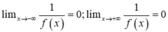 
⇒ y = 0 là tiệm cận ngang duy nhất.
Và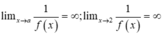 
⇒ x = a ; x = 2 là các đường tiệm cận đứng.
Vậy đồ thị hàm số có tổng 3 đường tiệm cận ngang và đứng.
Chọn đáp án B.
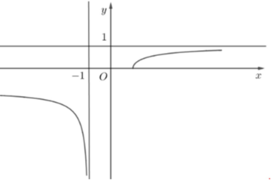
Quan sát đồ thị có 
là tiệm cận đứng và tiệm cận ngang của đồ thị hàm số đã cho.
Chọn đáp án A.
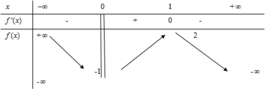
TCN: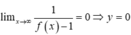
là tiệm cận ngang duy nhất;
TCĐ: Hàm số xác định ⇔ f ( x ) - 1 # 0 ⇔ f ( x ) # 1
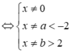
(vì đồ thị f(x) cắt đường thẳng y = 1 tại ba điểm có hoành độ lần lượt x=a<-2;x=0;x=b>2).
Có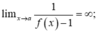 
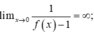
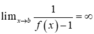
⇒ x = a ; x = 0 ; x = b là tiệm cận đứng.
Vậy đồ thị hàm số y = 1 f ( x ) - 1 có tổng 4 đường tiệm cận đứng và ngang.
Chọn đáp án B.
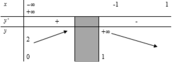
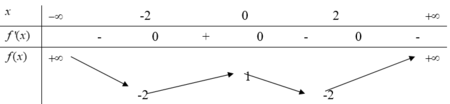
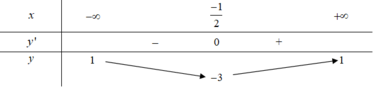
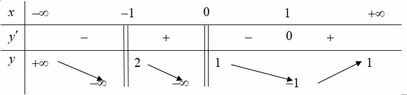
Đáp án C
Sử dụng định nghĩa về tiệm cận ta thấy các đáp án A, B, D là sai!