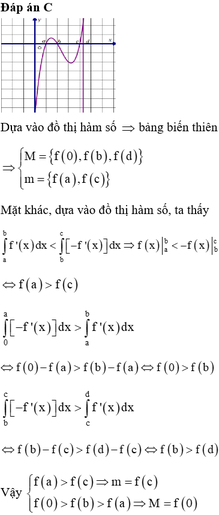Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Đáp án C
Phương pháp : Xét từng mệnh đề.
Cách giải:
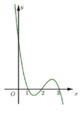
(I) sai. Ví dụ hàm số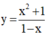 
có đồ thị hàm số như sau:
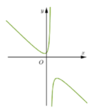õ ràng 
(II) đúng vì y ' = 4 a x 3 + 2 b x = 0 luôn có một nghiệm x = 0 nên đồ thị hàm số y = a x 4 + b x 2 + c ( a ≠ 0 ) luôn có ít nhất một điểm cực trị
(III) Gọi
x
0
là 1 điểm cực trị của hàm số 
=> Phương trình tiếp tuyến của đồ thị hàm số tại điểm có hoành độ
x
0
là: 
luôn song song với trục hoành.
Vậy (III) đúng.
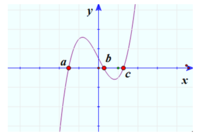
Đáp án D
Trên khoảng ( a ; b ) và ( c ; + ∞ ) hàm số đồng biến vì y'>0 đồ thị nằm hoàn toàn trên trục Ox
Hàm số nghịch biến trên các khoảng ( - ∞ ; a ) và (b;c) vì y'<0
Suy ra x=b là điểm cực đại mà y(b) <0 do đó trục hoành cắt đồ thị tại hai điểm phân biệt. Với d<0 ta có
Đáp án A
Hàm số f(x) xác định trên D⊆ R
Điểm
x
0
∈ D được gọi là điểm cực đại của hàm số f(x) nếu tồn tại một khoảng (a;b)⊂ D sao cho
x
0
∈ (a;b) và f(
x
0
)>f(x),∀x ∈ (a,b)∖{
x
0
}.
Đáp án A
Hàm số f(x) xác định trên D⊆ R
Điểm xo∈ D được gọi là điểm cực đại của hàm số f(x) nếu tồn tại một khoảng (a;b)⊂ D sao cho xo∈ (a;b) và f(xo)>f(x),∀x ∈ (a,b)∖{xo}.
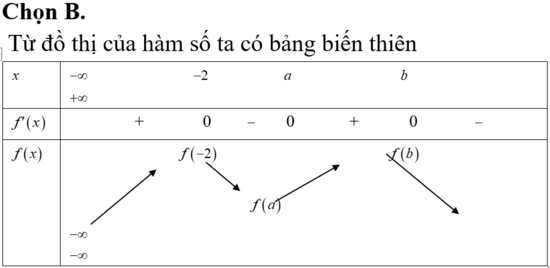
Đáp án B
Phương pháp: Từ đồ thị hàm số y = f’(x) lập BBT của đồ thị hàm số y = f(x) và kết luận.
Cách giải: Ta có 
BBT:
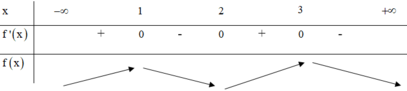
Từ BBT ta thấy (I) đúng, (II) sai.
Với 
=> Hàm số y = f(x+1) nghịch biến trên khoảng (0;1).
=>(III) đúng.
Vậy có hai khẳng định đúng
Đáp án B.
Ta có: Tập xác định của hàm số y = x 2 3 + 2017 là R nên y ' = 2 3 x 3
Ta có bảng biến thiên
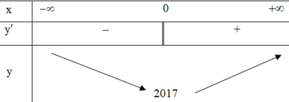
(I) sai vì hàm số chỉ đồng biến trên 0 ; + ∞ ;
(II) đúng là hàm số đạt cực tiểu x = 0; EM NHÌN KĨ BẢNG BIẾN THIÊN NHÉ!
(III) sai vì giá trị nhỏ nhất của hàm số là 2017
(IV) sai vì hàm số nghịch biến trên − ∞ ; 0
Lỗi sai
Ø Có bạn sẽ nhìn nhanh và nhầm y ' = 2 3 x 3 > 0 và kết luận là I đúng
Ø Có bạn sẽ không xét tại x = 0 vì tại đó y' không xác định. Hàm số vẫn đạt cực tiểu tại x = 0. Ta xét các điểm cực trị làm y' = 0 hoặc y' không xác định.
