Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Để đồ thị hàm số y = 3x + 1 đi qua A có hoành độ bằng \(\dfrac{2}{3}\) thì :
=> \(y=3\cdot\dfrac{2}{3}+1=3\)
Vậy tung độ của điểm A là 3
b) Với x nguyên dương :
\(P=\dfrac{\left|x+5\right|+6}{\left|x+5\right|+4}=\dfrac{x+5+6}{x+5+4}=\dfrac{x+11}{x+9}=\dfrac{x+9+2}{x+9}=1+\dfrac{2}{x+9}\)
Để P max <=> \(\dfrac{2}{x+9}max\Leftrightarrow x+9\) min <=> x min
Mà x là số nguyên dương <=> x = 1
Vậy MaxP = \(1+\dfrac{2}{1+9}=\dfrac{6}{5}\Leftrightarrow x=1\)
Gọi tung đọ của A là x
hoành độ của A là y
theo bài ra ta có y= 3x +1
=> y= 3\(\dfrac{2}{3}+1\)
=> y= 2 +1
=> y= 3
vậy tung độ của A là 3
b, x là \(\dfrac{2}{3}\)
=> P = (/ \(\dfrac{\left(\dfrac{2}{3}+5\right)+6}{\left(\dfrac{2}{3}+5\right)+4}\)
=> P =\(\dfrac{35}{39}\)

các bn làm ơn giúp mk giải bài toán này ik mk đag cần nó gấp :(

Bài 2:
\(3x^2+5\ge5>0\forall x\)
nên f(x)>0 với mọi x

Vẽ đồ thị giùm nha! Giúp câu chứng minh thôi. Ở đây vẽ đồ thị xấu lém =,=
Ta có: \(y=f\left(x\right)=3x^2+5\)
Ta có: \(x^2\ge0\forall x\) (luôn đúng)
Nên \(3x^2\ge0\). do đó \(y=f\left(x\right)=3x^2+5\ge5\forall x\)
Vậy hàm số \(y=f\left(x\right)=3x^2+5\) luôn dương với mọi x. (đpcm)
Vẽ đồ thị của hàm số y = f(x) = 1,5x. Bằng đồ thị, hãy tìm: Các giá trị của x khi y dương; khi y âm.

Vẽ đồ thị hàm số:
Vẽ hệ trục tọa độ Oxy
Với x= 2 thì y = 1,5. 2 = 3 ta được điểm A(2; 3)
Vẽ đường thẳng đi qua O, A ta được đồ thị hàm số y = f(x) = 1,5x
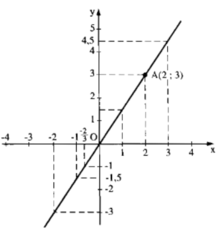
- Khi y dương: y > 0 ⇒ 1,5x > 0 ⇒ x > 0
- Khi y âm: y < 0 ⇒ 1,5x < 0 ⇒ x < 0
giúp mình với ạ
b: Để y dương thì -3x>0
hay x<0