Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn C
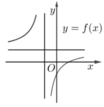
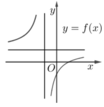
Nhìn vào đồ thị, ta thấy:.
Đồ thị cắt trục hoành tại điểm có hoành độ dương ![]()
Suy ra ab < 0
Đồ thị có tiệm cận đứng ![]()
Đồ thị có tiệm cận ngang ![]()
Từ (1) và (2) ta có ![]()

Đáp án: B.
Xét f(x) = x 3 + m x 2 + x - 5
Vì 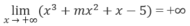
và f(0) = -5 với mọi m ∈ R cho nên phương trình f(x) = 0 luôn có nghiệm dương.

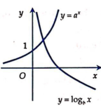
Chọn A
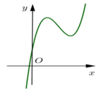
Đồ thị cắt trục tung tại điểm (0;c), từ đồ thị suy ra c < 0
Mặt khác đồ thị hàm số có ba điểm cực trị nên y' = 0 có ba nghiệm phân biệt, hay ![]() có ba nghiệm phân biệt. Suy ra a,b trái dấu.
có ba nghiệm phân biệt. Suy ra a,b trái dấu.
Mà a < 0 => b > 0
Vậy chọn A
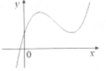




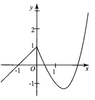
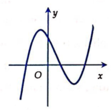
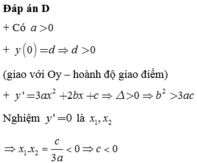
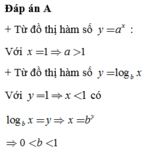
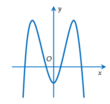
Vì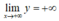 nên a > 0. Đồ thị cắt trục Oy tại điểm nằm trên trục hoành nên d > 0.
nên a > 0. Đồ thị cắt trục Oy tại điểm nằm trên trục hoành nên d > 0.
Pt y' = 0 có 2 nghiệm dương phân biệt nên:
Do đó ac > 0, bd < 0.
Chọn A