Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

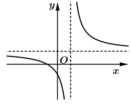
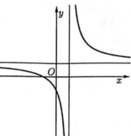
Đồ thị hàm số có tiệm cận đứng x = a > 0; tiệm cận ngang y = b > 0
Mặt khác, ta thấy dạng đồ thị là đường cong đi xuống từ trái sang phải trên các khoảng xác định của nó nên
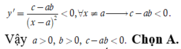

Nhận xét:
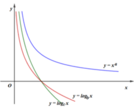
+) Đồ thị hàm số y = x a nghịch biến trên khoảng ( 0 ; + ∞ ) ⇒ a < 0
+) Xét đồ thị hàm số y = log b x v à y = log c x , x > 0
Cho y=1 ta có: log b x 1 = log c x 2 ⇔ x 1 = b , x 2 = c
Mà x 1 < x 2 ⇒ b < c ⇒ a < 0 < b < c . Vậy a<b<c
Chọn đáp án D.

Đáp án D
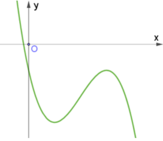
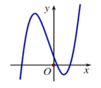
Đồ thị hàm số đi từ dưới lên ⇒ a < 0 .
Đồ thị có 2 điểm cực trị đạt được tại hoành độ trái dấu và tổng nhỏ hơn 0 nên ta có c a < 0 ⇒ c < 0
Và – b a 0 ⇒ b 0
Đồ thị hàm số cắt trục tung tại điểm dương ⇒ d > 0 .
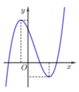

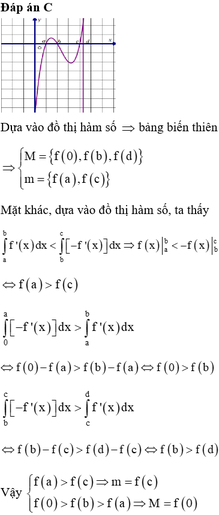
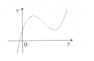







Đáp án D
Dựa vào hình vẽ, ta thấy rằng:
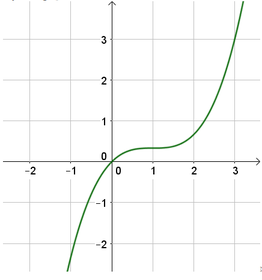
lim x → − ∞ y = − ∞ ; lim x → + ∞ y = + ∞ → Hệ số a > 0.
Đồ thị hàm số cắt trục Oy tại điểm có tung độ dương ⇒ y 0 = d > 0.
Hàm số có 2 điểm cực trị x 1 , x 2 thỏa mãn
x 1 + x 2 = − 2 b 3 a > 0 x 1 x 2 = c 3 a < 0 ⇔ b < 0 c < 0 .
Vậy a , d > 0 , b , c < 0.