Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a.
Hệ số a: -2
Hệ số b: 4
Do hệ số a nhỏ hơn 0 (-2<0) => Hàm số nghịch biến
b.
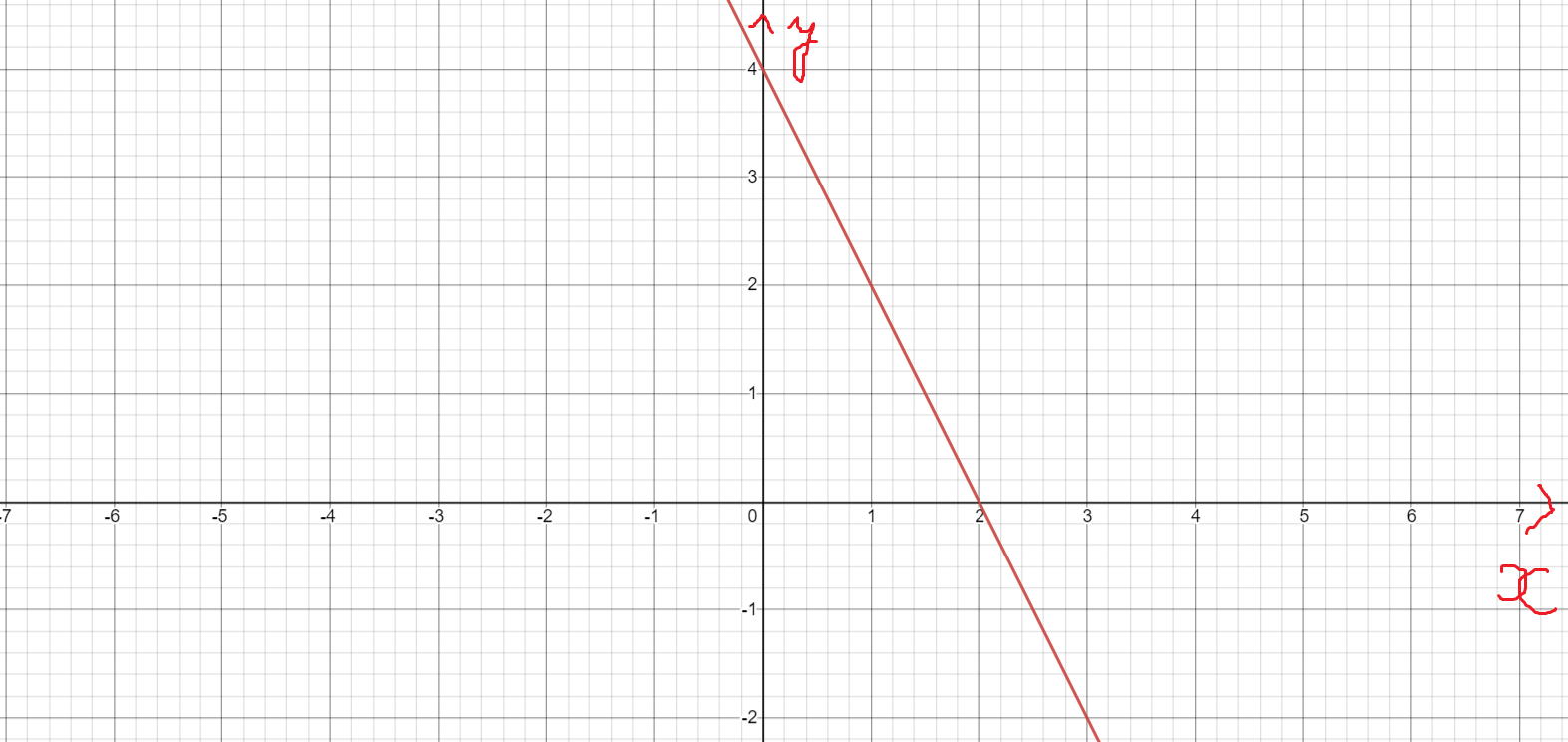

a, Vì \(a=1>0\) nên đths đồng biến trên R
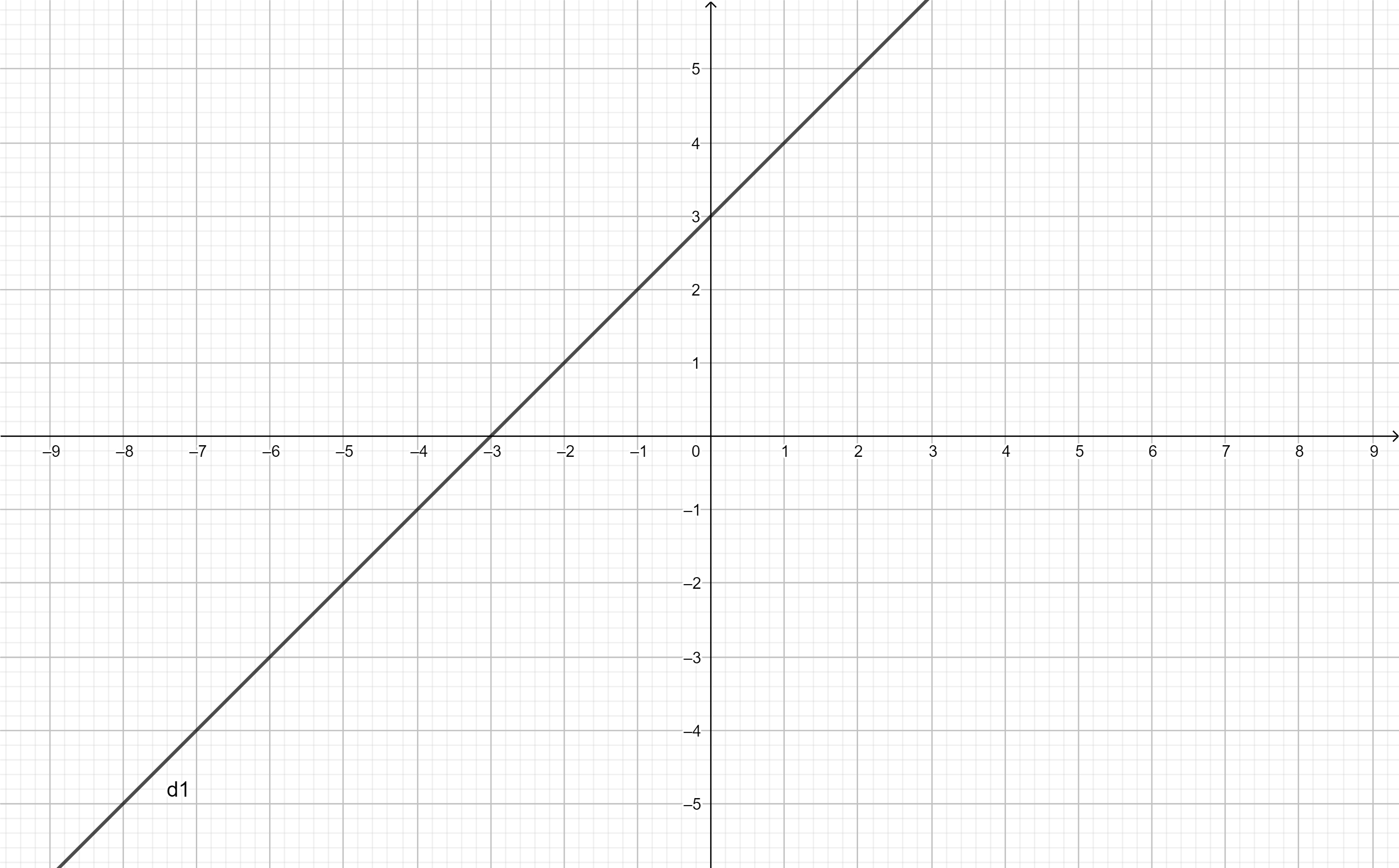
b, Vì (d1)//(d2) nên \(\left\{{}\begin{matrix}a=1\\b\ne3\end{matrix}\right.\)
Vì (d2) cắt trục hoành tại hoành độ 2 nên \(y=0;x=2\)
\(\Leftrightarrow0=2a+b=2+b\Leftrightarrow b=-2\left(tm\right)\)
Vậy đths là \(\left(d_2\right):y=x-2\)

a: Hàm số đồng biến khi x>0 và nghịch biến khi x<0
b: 
c: PTHĐGĐ là:
2x^2=x+1
=>2x^2-x-1=0
=>2x^2-2x+x-1=0
=>(x-1)(2x+1)=0
=>x=1 hoặc x=-1/2
=>y=2 hoặc y=1/2

\(b,\) PT giao Ox và Oy:
\(y=0\Leftrightarrow x=2\Leftrightarrow A\left(2;0\right)\Leftrightarrow OA=2\\ x=0\Leftrightarrow y=-4\Leftrightarrow B\left(0;-4\right)\Leftrightarrow OB=4\)
Gọi H là chân đường cao từ O đến (d)
Áp dụng HTL: \(\dfrac{1}{OH^2}=\dfrac{1}{OA^2}+\dfrac{1}{OB^2}=\dfrac{1}{4}+\dfrac{1}{16}=\dfrac{5}{16}\)
\(\Leftrightarrow OH^2=\dfrac{16}{5}\Leftrightarrow OH=\dfrac{4}{\sqrt{5}}\left(cm\right)\)
Vậy k/c là \(\dfrac{4}{\sqrt{5}}\left(cm\right)\)
\(c,\Leftrightarrow\left\{{}\begin{matrix}a=2;b\ne-4\\0a+b=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=2\\b=3\end{matrix}\right.\)

c: Thay x=1 và y=1 vào hàm số, ta được:
y=2x1-3=-1<>1
Vậy: Điểm M ko thuộc đồ thị
b: Hàm số đồng biến vì a=2>0

a) - Với hàm số y = 2x
Bảng giá trị:
| x | 0 | 1 |
| y = 2x | 0 | 2 |
Đồ thị hàm số y = 2x đi qua gốc tọa độ và điểm A( 1;2)
- Với hàm số y = -2x
Bảng giá trị:
| x | 0 | 1 |
| y = -2x | 0 | -2 |
Đồ thị hàm số y = -2x đi qua gốc tọa độ và điểm B( 1; - 2)
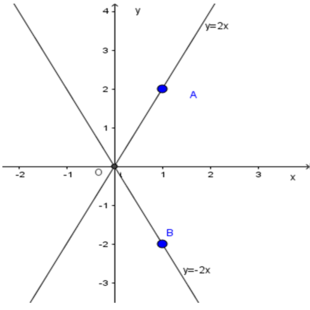
b) - Ta có O ( x 1 = 0 , y 1 = 0 ) và A( x 2 = 1 , y 2 = 2 ) thuộc đồ thị hàm số y = 2x, nên với x 1 < x 2 ta được f ( x 1 ) < f ( x 2 ) .
Vậy hàm số y = 2x đồng biến trên R.
- Lại có O( x 1 = 0 , y 1 = 0 ) và B ( x 3 = 1 , y 3 = - 2 ) thuộc đồ thị hàm số y = -2x, nên với x 1 < x 3 ta được f ( x 1 ) < f ( x 3 ) .
Vậy hàm số y = -2x nghịch biến trên R.
Hệ số a: -2. \(\Rightarrow\) Hàm số nghịch biến.
Hệ số b: 4.