Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn C
Do các đặc điểm đồ thị cảu hàm trùng phương nên khi đồ thị hàm số có 3 điểm cực thị thì hiển nhiên 3 điểm này tạo thành 3 đỉnh của một tam giác cân.
Yêu cầu bài toán tương đương .
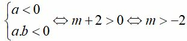

Đáp án A
Phương pháp giải:
Tìm tọa độ điểm cực trị của đồ thị hàm số trùng phương và tính diện tích tam giác
Lời giải: TXĐ : D = R
Ta có ![]() R
R
Phương trình 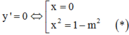
Hàm số có 3 điểm cực trị ó (*) có 2 nghiệm phân biệt khác ![]()
Khi đó 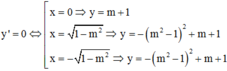
Gọi ![]() ;
; ![]() là ba điểm cực trị. Tam giác ABC cân tại A.
là ba điểm cực trị. Tam giác ABC cân tại A.
Trung điểm H của BC là ![]()
![]()
Và ![]()
Diện tích tam giác ABC là ![]()
![]()
Mà ![]() R suy ra
R suy ra ![]()
Vậy Smax = 1 Dấu bằng xảy ra khi và chỉ khi m = 0






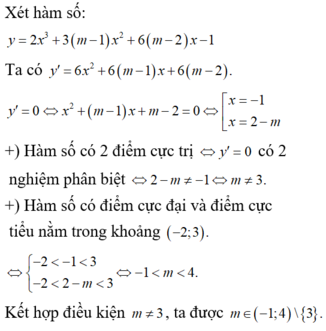



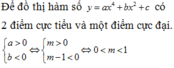


Đáp án B.
Ta có y ' = 2 x 2 + 2 m + 1 x + m 2 + 4 m + 3 ; ∀ x ∈ ℝ .
Phương trình y ' = 0 ⇔ 2 x 2 + 2 m + 1 x + m 2 + 4 m + 3 = 0 (*).
Để hàm số đã cho có 2 điểm cực trị ⇔ (*) có 2 nghiệm phân biệt ⇔ ∆ ' > 0 ⇔ - 5 < m < - 1 .
Và các điểm cực trị của hàm số nằm bên phải Oy ⇔ m 2 + 4 m + 3 > 0 ⇔ [ m > - 1 m < - 3 .
Vậy - 5 < m < - 3 là giá trị cần tìm.