Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn D
Xét hàm số ![]() .
.
Có ![]()
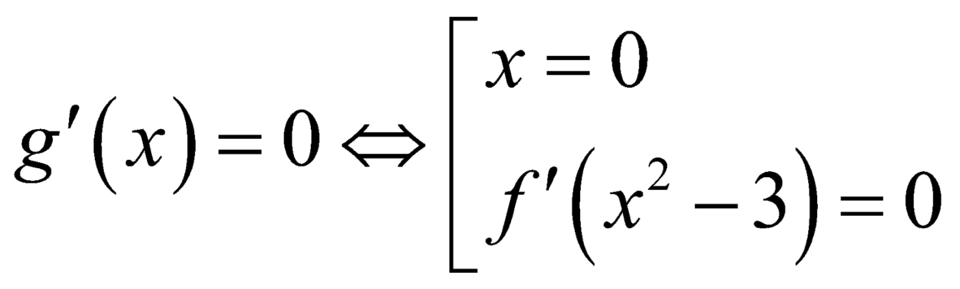
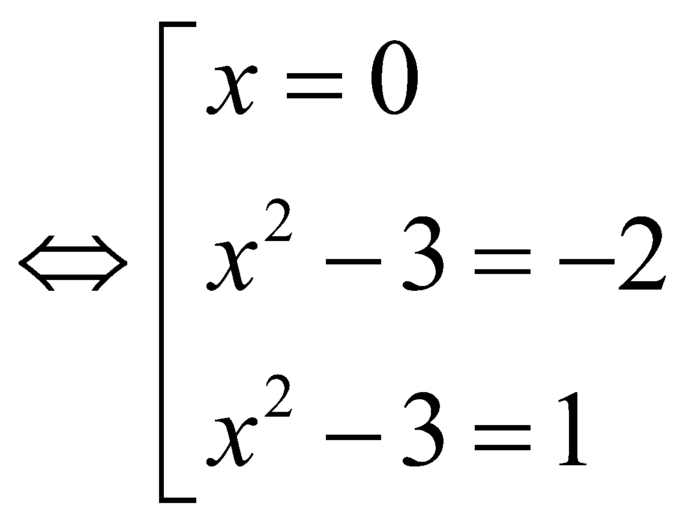
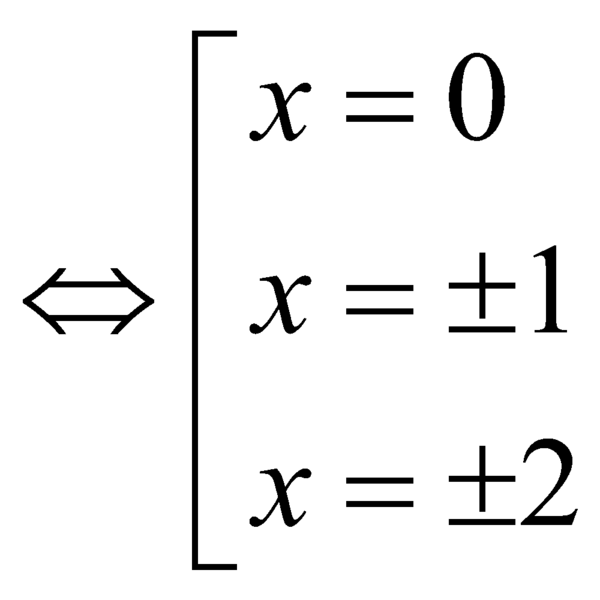 .
.
Ta lại có ![]() thì
thì ![]() . Do đó
. Do đó ![]() thì
thì ![]() .
.
![]() thì
thì ![]() . Do đó
. Do đó ![]() thì
thì ![]() .
.
Từ đó ta có bảng biến thiên của ![]() như sau
như sau
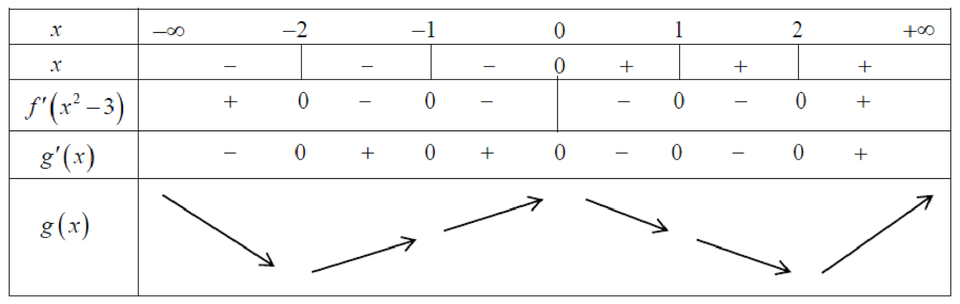
Dựa vào bảng biến thiên, ta có
I. Hàm số ![]() có 3 điểm cực trị . LÀ MỆNH ĐỀ ĐÚNG.
có 3 điểm cực trị . LÀ MỆNH ĐỀ ĐÚNG.
II. Hàm số ![]() đạt cực tiểu tại
đạt cực tiểu tại ![]() LÀ MỆNH ĐỀ SAI.
LÀ MỆNH ĐỀ SAI.
III. Hàm số ![]() đạt cực đại tại
đạt cực đại tại ![]() LÀ MỆNH ĐỀ SAI.
LÀ MỆNH ĐỀ SAI.
IV. Hàm số ![]() đồng biến trên khoảng
đồng biến trên khoảng ![]() LÀ MỆNH ĐỀ ĐÚNG.
LÀ MỆNH ĐỀ ĐÚNG.
V. Hàm số ![]() nghịch biến trên khoảng
nghịch biến trên khoảng ![]() LÀ MỆNH ĐỀ SAI.
LÀ MỆNH ĐỀ SAI.
Vậy có hai mệnh đề đúng.
ở chỗ x<1=> x= -2 thì sao bạn ơi =>(x^2 -3) =1 >0 thì sao f ' (...)>0 được ????

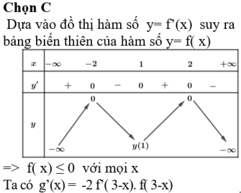
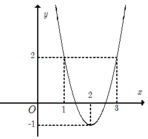
Dựa vào đồ thị hàm số ta thấy: f’(x) = 0 khi và chỉ khi x= 1; ![]()
Ta có bảng biến thiên :
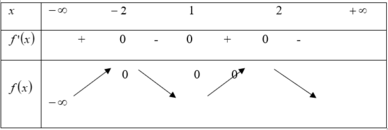
Dựa vào bảng biến thiên ta thấy f(x) < 0 với mọi x≠ ± 2
Xét hàm số y= ( f( x) ) 2 có đạo hàm y’ = 2f(x). f’ (x)
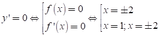
Bảng xét dấu:
Chọn D.

Chọn D
i) Đúng.
ii) Sai, ví dụ: Xét hàm số
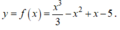
Ta có f ' x = x 2 - 2 x + 1 .
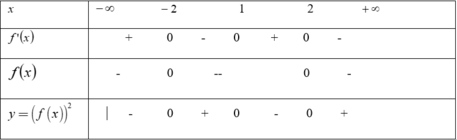
Cho f ' ( x ) ⇔ x = 1 .
Khi đó phương trình f ' ( x ) = 0 có nghiệm x 0 = 1 nhưng đây là nghiệm kép nên không đổi dấu khi qua x 0 .
iii) Sai, vì: Thiếu điều kiện f ' ( x ) = 0 chỉ tại một số hữu hạn điểm.
Vậy có 1 mệnh đề đúng.

Phương pháp:
Sử dụng cách đọc đồ thị hàm số.
Cách giải:
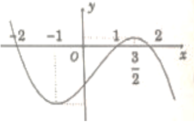
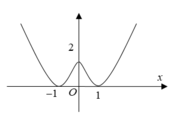
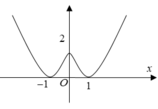
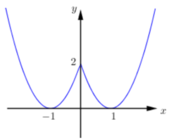
Từ đồ thị hàm số ta thấy
+ Đồ thị đi xuống trên khoảng 0;1
nên Hàm số nghịch biến trên
khoảng 0;1. Do đó (I) đúng
+ Đồ thị đi lên trên khoảng 1;0,
đi xuống trên khoảng 0;1và đi
lên trên khoảng 1;2 nên trên
khoảng 1;2 hàm số không
hoàn toàn đồng biến. Do đó (II) sai.
+ Đồ thị hàm số có ba điểm hai
điểm cực tiểu và một điểm cực
đại nên (III) đúng.
+ Giá trị lớn nhất của hàm số là
tung độ của điểm cao nhất của đồ
thị hàm số nên (IV) sai.
Như vậy ta có hai mệnh đề đúng
là (I) và (III).
Chọn B.
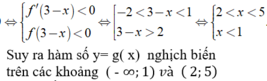


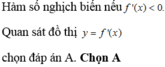
Chọn C
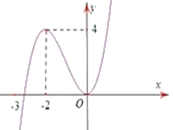
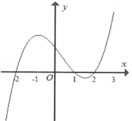
Trên khoảng ( - 3; + ∞) ta thấy đồ thị hàm số y= f’( x) nằm trên trục hoành.
=> Trên khoảng ( - 3; + ∞) thì f’(x)>0.
=> Trên khoảng ( - 3; + ∞) thì hàm số y= f(x) đồng biến.