Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Nếu hàm số y = f(x) liên tục trên đoạn [a; b] và f(a).f(b) > 0 thì phương trình f(x) = 0 có thể có nghiệm hoặc vô nghiệm trong khoảng (a; b)
Ví dụ minh hoạ :
- f ( x ) = x 2 − 1 liên tục trên đoạn [−2;2], f(−2).f(2) = 9 > 0
Phương trình x 2 – 1 = 0 có nghiệm x = 1 hoặc x = -1 trong khoảng (-2; 2)
- f ( x ) = x 2 + 1 liên tục trên đoạn [-1; 1] và f(−1).f(1) = 4 > 0. Còn phương trình x 2 + 1 = 0 lại vô nghiệm trong khoảng (-1; 1)

Nếu hàm số y = f(x) không liên tục trên đoạn [a; b] nhưng f(a).f(b) < 0 thì phươngtrình f(x) = 0 có thể có nghiệm hoặc vô nghiệm trong khoảng (a; b)
Minh hoạ hình hoạ (H.8):
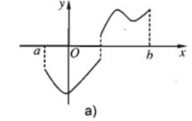
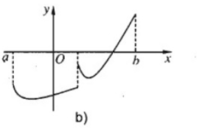

Chọn C.
- Hàm số g(x) = f(x) - x xác định và liên tục trên đoạn [a ; b].
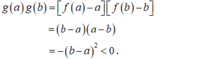
- Suy ra: phương trình f(x) – x = 0 luôn có nghiệm trên khoảng (a, b).

Đặt 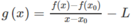
Suy ra g(x) xác định trên
(
a
;
b
)
\
x
0
và 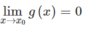
Mặt khác, f ( x ) = f ( x 0 ) + L ( x − x 0 ) + ( x − x 0 ) g ( x ) nên
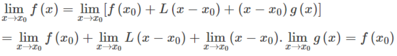
Vậy hàm số y = f(x) liên tục tại



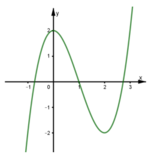

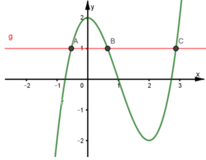




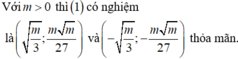
Chọn D.
- Theo lý thuyết.