Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Đáp án là B
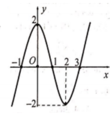
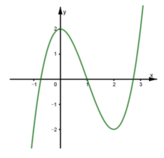
Từ đồ thị hàm số và phương trình f(x) = 1 có ba số thực a,b,c thỏa
-1 < a < 1 < b < 2 < c sao cho f(a) = f(b) = f(c) = 1. Do đó,
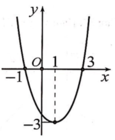
Dựa vào đồ thị hàm số y = f(x) ta có:
Do -1 < a < 1 nên đường thẳng y = a cắt đồ thị hàm số y = f(x) tại 3 điểm phân biệt. Do đó, f(x) = a có 3 nghiệm phân biệt.
Ta lại có, 1 < b < 2 nên đường thẳng y = b cắt đồ thị hàm số y = f(x) tại 3 điểm phân biệt khác. Do đó, f(x) = b có 3 nghiệm phân biệt khác các nghiệm trên.
Ngoài ra, 2 < c nên đường thẳng y = b cắt đồ thị hàm số y = f(x) tại 1 điểm khác các điểm trên. Hay f(x) = c có 1 nghiệm khác các nghiệm trên.
Từ đó, số nghiệm của phương trình f(f(x)) = 1 là m = 7
Chọn A
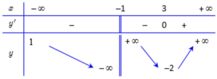
Đáp án A sai vì hàm số xác định trên ℝ \{-1} nên hàm số nghịch biến trên (- ∞ ;-1) và (-1;3).
Chọn A.
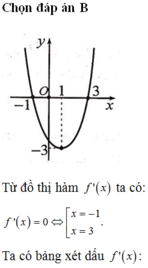
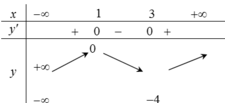
Dựa vào BBT, ta thấy hàm số đạt cực tiểu tại x = 3 và đạt cực đại tại x = 1 nên loại phương án C. Hàm số y = f ( x ) xác định, liên tục trên ℝ ; y ' đổi dấu và lim x → ± ∞ = ± ∞ nên hàm số không tồn tại giá trị lớn nhất và giá trị nhỏ nhất nên loại phương án B. Hàm số có giá trị cực tiểu là y C T = - 4 và giá trị cực đại là y C D = 0 nên loại phương án D.
Chọn A.
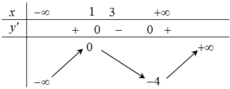
Dựa vào BBT, ta thấy hàm số đạt cực tiểu tại x = 3 và đạt cực đại tại x = 1 nên loại phương án C. Hàm số y = f ( x ) xác định, liên tục trên ℝ ; y ' đổi dấu và lim x → ± ∞ y = ± ∞ nên hàm số không tồn tại giá trị lớn nhất và giá trị nhỏ nhất nên loại phương án B. Hàm số có giá trị cực tiểu là y C T = - 4 và giá trị cực đại là y C D = 0 nên loại phương án D.
vô nghiệm.
có ít nhất một nghiệm trên khoảng 
.
có hai nghiệm 
.
vô nghiệm.
Chọn B
Đặt 
.
Vì
liên tục trên đoạn 
nên 
liên tục trên 
.Ta xét các trường hợp sau:
+ Với 
.
Ta có: 
.
Suy ra phương trình 
có ít nhất một nghiệm trên khoảng 
.
Vậy A sai.
+ Với 
.
Ta có: 
.
Suy ra phương trình 
có ít nhất một nghiệm trên khoảng 
.
Vậy B đúng, D sai.
+ Với 
.
Ta có: 
Suy ra 
không là nghiệm của phương trình 
hay 
.
Vậy C sai.
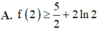
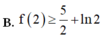
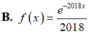
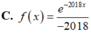
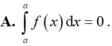
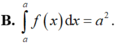
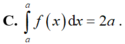
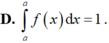
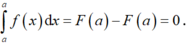
Đáp án B