Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn C.
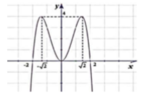
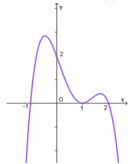
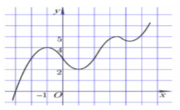
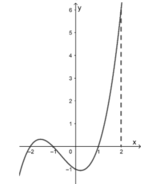
Dựa vào đồ thị ta thấy trên đoạn [0;2] hàm số f(x) có giá trị lớn nhất bằng 4 khi x = 2
Suy ra M a x [ 0 ; 2 ] f ( x ) = 4

Chọn A
+ Từ đồ thị của đạo hàm ta lập được bảng biến thiên như sau
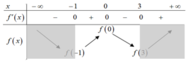
+ Dựa vào BBT ta suy ra giá trị lớn nhất của hàm số trên đoạn [-1;3] là f(0)

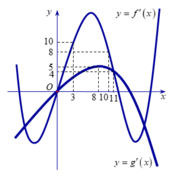
Chọn B
Ta có: ![]()
![]()

Từ đồ thị ta cáo bảng xét dấu
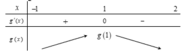
Giá trị lớn nhất của hàm số g(x) = f(x) - 1 3 x 3 + x - 1 trên đoạn [-1;2] bằng f(1) - 1 3

Chọn A
Dựa vào đồ thị của hàm f'(x) ta có bảng biến thiên.
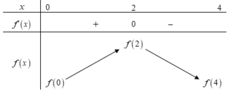
Vậy giá trị lớn nhất M = f(2)
Hàm số đồng biến trên khoảng (0;2) nên f(2) > f(1) => f(2) - f(1) > 0 .
Hàm số nghịch biến trên khoảng (2;4) nên f(2) > f(3) => f(2) - f(3) > 0.
Theo giả thuyết: f(0) + f(1) - 2f(2) = f(4) - f(3).
![]()
=> f(0) > f(4)
Vậy giá trị nhỏ nhất m = f(4)

Chọn A
Từ đồ thị của hàm số y = f'(x) ta có bảng biến thiên của hàm số y = f(x) trên đoạn [-1;2] như sau
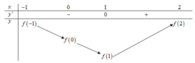
Nhận thấy
![]()
Để tìm ![]() ta so sánh f(-1) và f(2)
ta so sánh f(-1) và f(2)
Theo giả thiết, ![]()
![]()
Từ bảng biến thiên , ta có f(0) - f(1) > 0. Do đó f(2) - f(-1) > 0 ![]()
![]()
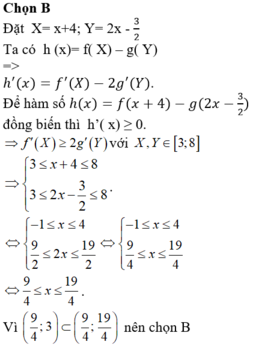
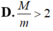

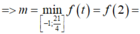
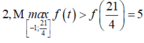



Lời giải:
$g(x)=2x-f(2x-1)$
$g'(x)=2-2f'(2x-1)=2[1-f'(2x-1)]=0$
$\Leftrightarrow f'(2x-1)=1$
$\Leftrightarrow x=0;x=1; x=\frac{3}{2}$
Lập bảng biến thiên với các mốc $0; 1;\frac{3}{2};2$ ta thấy $g(x)$ đạt max tại $x=\frac{3}{2}$, tức là $g(x)_{\max}=-f(2)+3$
Em cũng làm như vậy nhưng đến bước BBT thì em lấy các giá trị trong các khoảng (0;1), (1;\(\dfrac{3}{2}\)), (\(\dfrac{3}{2}\);2) thay vào biểu thức f ' (2x-1) = 1 để xét dấu thì không ra như đáp án ạ.
Không biết em có sai ở đâu không ạ?