K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên

NV
Nguyễn Việt Lâm
Giáo viên
28 tháng 2 2021
\(g\left(x\right)=f\left(1-2018x\right)\Rightarrow g'\left(x\right)=-2018f'\left(1-2018x\right)\)
\(\Rightarrow\) Số nghiệm của \(g'\left(x\right)\) bằng số nghiệm \(f'\left(x\right)\Rightarrow g'\left(x\right)\) có 4 nghiệm
\(g\left(x\right)=0\Leftrightarrow f\left(1-2018x\right)=0\) có số nghiệm bằng số nghiệm f(x)
Do \(f'\left(x\right)\) có 4 nghiệm nên f(x) có tối đa 5 nghiệm
Vậy hàm có tối đa 9 cực trị



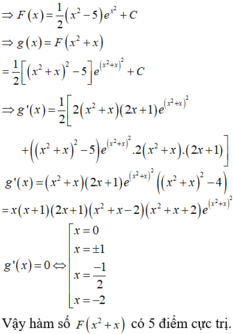
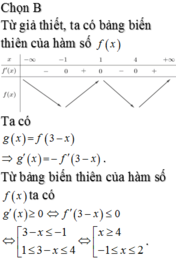
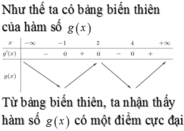


câu này là tìm cực đại mà??? Nếu vậy chỉ cần vẽ bảng biến thiên rồi đếm số điểm cực đại đúng ko???
Bài này khá dễ, chỉ cần tìm số nghiệm bội lẻ và dương của \(f'\left(x\right)=0\), gọi nó là k thì số cực trị của \(f\left(\left|x\right|\right)=2k+1\) (do đồ thị đối xứng qua Oy đồng thời luôn nhận \(x=0\) là 1 cực trị)
\(f'\left(x\right)=0\) có các nghiệm bội lẻ dương là 2; 3; 7; 25 tổng cộng 4 nghiệm
Do đó \(f\left(\left|x\right|\right)\) có 9 cực trị