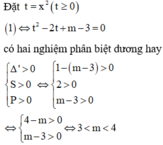

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.





Đáp án C.
Phương trình có hoành độ giao điểm của d và (C):
x 3 + 2 m x 2 + ( m + 3 ) x + 4 = x + 4 ⇔ x 2 + 2 m x + ( m + 2 ) = 0
Để d cắt (C) tại 3 điểm phân biệt A(0;4) và C thì phương trình (*) phải có hai nghiệm phân biệt x 1 , x 2 khác 0
⇔ 0 2 + 2 m . 0 + m + 2 ≢ 0 ∆ ' = m 2 - m - 2 > 0 ⇔ m + 2 ≢ 0 ( m + 1 ) ( m - 2 ) > 0 ⇔ m ≢ - 2 m > 2 m < - 1 ⇔ m > 2 m < - 1 m ≢ - 2 (1)
Giả sử B x 1 ; x 1 + 4 và B x 2 ; x 2 + 4 với x 1 , x 2 là hai nghiệm của (*)
Suy ra B C = 2 x 1 - x 2 và theo định lí Vi-ét: x 1 + x 2 = - 2 m x 1 x 2 = m + 2
Ta có S ∆ M B C = 1 2 d ( M ; B C ) . B C = 1 2 . 1 - 3 + 4 2 . 2 x 1 - x 2 = x 1 - x 2
Từ giả thiết ta có S ∆ M B C = 4 ⇔ x 1 - x 2 = 4 ⇔ x 1 - x 2 2 = 16
⇔ x 1 + x 2 2 - 4 x 1 x 2 = 16 ⇔ ( - 2 m ) 2 - 4 ( m + 2 ) - 16 = 0 ⇔ 4 m 2 - 4 m - 24 = 0
m = - 2 m = 3 . Đối chiếu với điều kiện (1), chỉ có m = 3 là thỏa mãn

Đáp án C
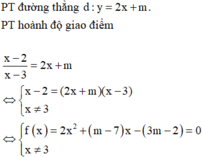
Để (C) cắt d tại 2 điểm phân biệt có hoành độ dương thì PT f(x) = 0 có 2 nghiệm dương phân biệt khác 3
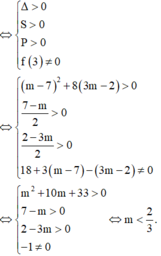

Đáp án D
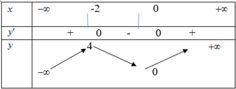
Trên khoảng ( a ; b ) và ( c ; + ∞ ) hàm số đồng biến vì y'>0 đồ thị nằm hoàn toàn trên trục Ox
Hàm số nghịch biến trên các khoảng ( - ∞ ; a ) và (b;c) vì y'<0
Suy ra x=b là điểm cực đại mà y(b) <0 do đó trục hoành cắt đồ thị tại hai điểm phân biệt. Với d<0 ta có

Đáp án B
Đồ thị hàm số y = x 4 - 2 x 2 - 3 + m cắt trục hoành tại 4 nghiệm phân biệt khi và chỉ khi
phương trình x 4 - 2 x 2 - 3 + m = 0 có 4 nghiệm phân biệt (1)