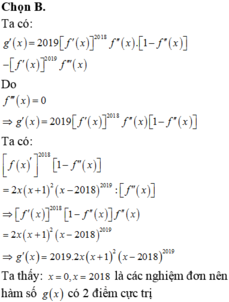Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B.
Phương pháp : Chuyển vế, lấy nguyên hàm hai vế.
Cách giải :
![]()
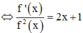
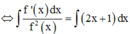
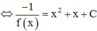
![]()
![]()
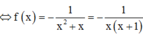
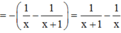
![]()
![]()
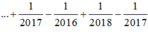
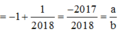
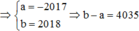

Đáp án A.
Lưu ý: Nếu c, d lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số
y = f x trên (m;n) thì giá trị lớn nhất của hàm số y = f x trên (m;n) là M a x a ; b .
Xét hàm số f x = 2 3 x 3 − 2 x 2 + 1. Ta có f ' x = 2 x 3 − 4 x = 2 x x − 2 . Ta có bảng biến thiên của hàm số trên − 8 3 ; 3 như sau:
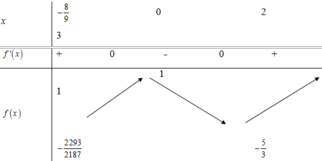
Dựa vào bảng biến thiên, ta thấy M i n f x = − 5 3 và M a x f x = 1 trên − 8 3 ; 3 .
Do đó
M = M a x − 5 3 ; 1 = 5 3 ⇒ a = 5 ; b = 3.
Do đó S = a + b 3 = 5 + 3 3 = 32.

Đáp án A.
Phương trình đã cho tương đương với:
2 x 2 + m x + 1 = x 2 + 6 x + 9 x ≥ − 3 ⇔ x 2 + m − 6 x − 8 = 0 1 x ≥ − 3
Để phương trình có hai nghiệm phân biệt thì (1) phải có 2 nghiệm phân biệt x 2 > x 1 ≥ − 3
⇔ Δ > 0 x 1 + x 2 ≥ − 6 x 1 + 3 x 2 + 3 ≥ 0 ⇔ m − 6 2 + 32 > 0 − m − 6 ≥ − 6 − 8 + 3. − m + 6 + 9 ≥ 0 ⇔ 6 − m ≥ − 6 19 − 3 m ≥ 0 ⇔ m ≤ 12 m ≤ 19 3 ⇔ m ≤ 19 3
Do đó
a b = 19 3 ⇒ a = 19 b = 3 ⇒ B = a 2 − b 3 = 19 2 − 3 3 = 334.