K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
CM
23 tháng 6 2017
Hàm số y = ax + 3 là hàm số bậc nhất nên a ≠ 0
a) Đồ thị của hàm số đi qua điểm A(2; 6) nên:
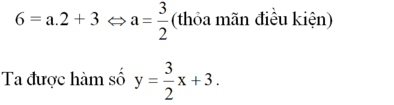
b) Vẽ đồ thị:
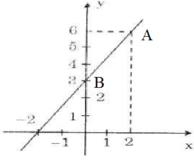
- Cho x = 0 thì y = 3 ta được B(0; 3).
Nối A, B ta được đồ thị hàm số
18 tháng 11 2021
\(a,\Leftrightarrow1-a=\dfrac{1}{2}\Leftrightarrow a=\dfrac{1}{2}\)
Hệ số góc: \(\dfrac{1}{2}\)
\(b,a=\dfrac{1}{2}\Leftrightarrow y=\dfrac{1}{2}x+1\)
CM
13 tháng 7 2017
Hàm số y = ax + 3 là hàm số bậc nhất nên a ≠ 0
Đồ thị của hàm số đi qua điểm A(2; 6) nên:
AH
Akai Haruma
Giáo viên
19 tháng 12 2022
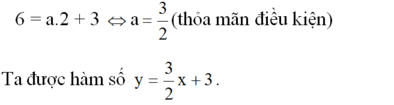
Lời giải:
a. ĐTHS đi qua $A(4;8)$ nên $y_A=ax_A+4$
$\Leftrightarrow 8=4a+4\Leftrightarrow a=1$
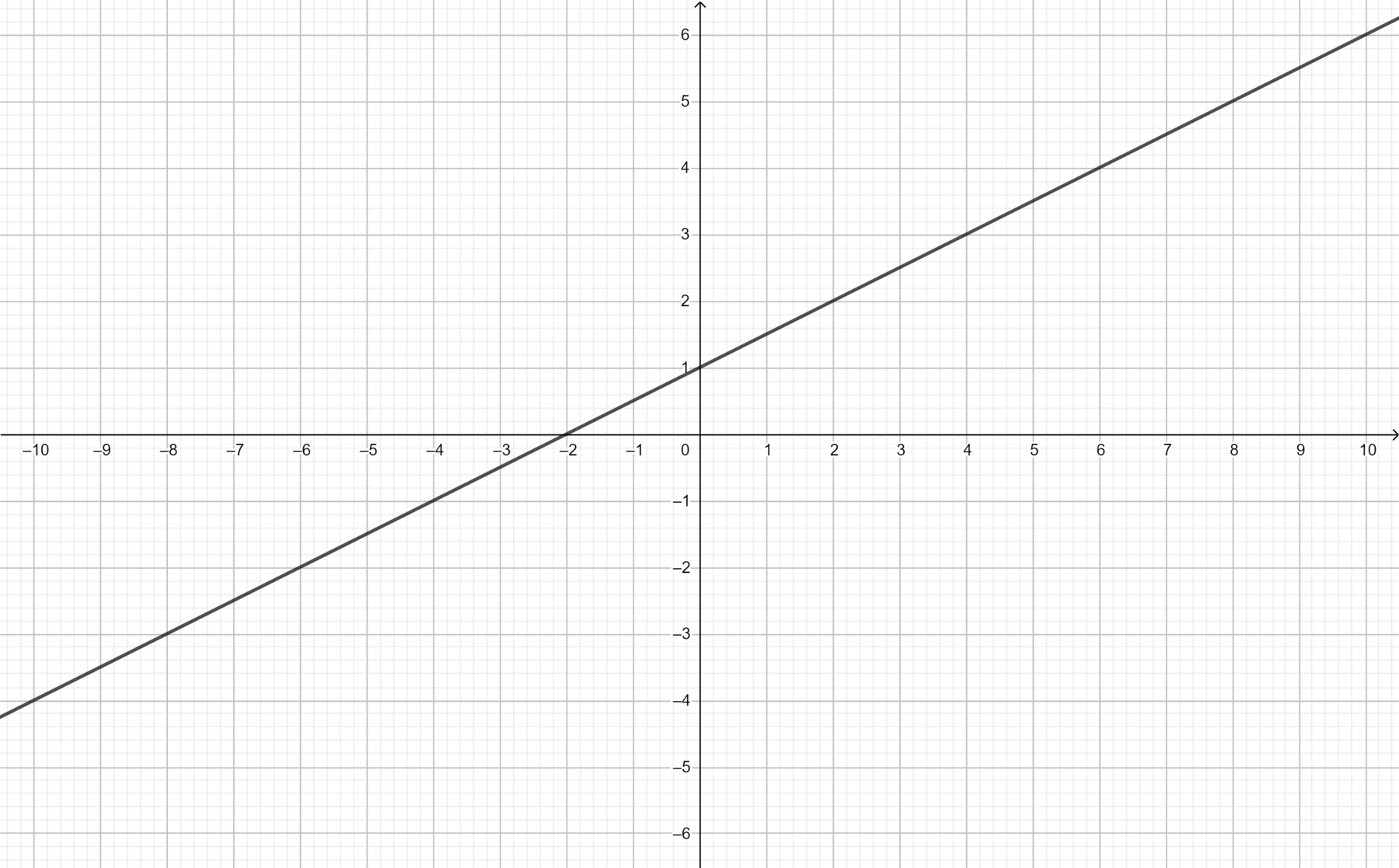
b. ĐTHS hàm số vừa tìm được là $y=x+4$
Với $x=0$ thì $y=0+4=4$. Ta có điểm $A(0;4)$
Với $x=1$ thì $y=1+4=5$. Ta có điểm $B(1;5)$
Nối $A,B$ ta có đths $y=x+4$
a) Vì đồ thi của hàm số đi qua điểm A(2; 6) nên ta có 6 = a.2 + 3.
Suy ra hệ số góc a = 3/2 và được hàm số y = 3/2x + 3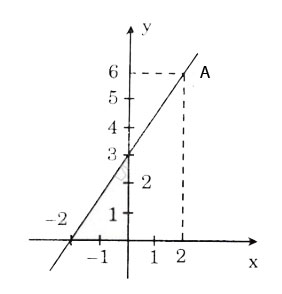
b) Hàm số đã cho là y = 3/2x + 3. Đồ thị được vẽ như hình bên.
Bài giải:
a) Vì đồ thi của hàm số đi qua điểm A(2; 6) nên ta có 6 = a . 2 + 3.
Suy ra hệ số góc a = 1, 5.
b) Hàm số đã cho là y = 1,5x + 3. Đồ thị được vẽ như hình bên.