Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi d: y=ax+ b
Đường thẳng d đi qua N( 1; -1) nên -1= a+ b
Và ![]() suy ra b= -2.
suy ra b= -2.
Vậy hàm số cần tìm là y= x-2.
Chọn B.

a) Vì đồ thị hàm số ax+b song song với (d1) nên a=3
hay hàm số có dạng là y=3x+b
Vì đồ thị hàm số y=3x+b đi qua điểm C(3;-2)
nên Thay x=3 và y=-2 vào hàm số y=3x+b, ta được:
\(3\cdot3+b=-2\)
\(\Leftrightarrow b+9=-2\)
hay b=-11
Vậy: Hàm số có dạng là y=3x-11
b) Vì (d)⊥(d2) nên \(a\cdot4=-1\)
hay \(a=-\dfrac{1}{4}\)
Vậy: Hàm số có dạng là \(y=-\dfrac{1}{4}x+b\)
Vì (d) đi qua D(2;-1) nên
Thay x=2 và y=-1 vào hàm số \(y=-\dfrac{1}{4}x+b\), ta được:
\(-\dfrac{1}{4}\cdot2+b=-1\)
\(\Leftrightarrow b-\dfrac{1}{2}=-1\)
hay \(b=-\dfrac{1}{2}\)
Vậy: \(a=-\dfrac{1}{4}\) và \(b=-\dfrac{1}{2}\)

Pt tọa độ giao điểm d1 và d2:
\(\left\{{}\begin{matrix}y=3x-5\\y=4x-9\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}3x-y=5\\4x-y=9\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x=4\\y=7\end{matrix}\right.\)
\(\Rightarrow M\left(4;7\right)\)
Do đồ thị hàm bậc 2 đã cho qua A và M nên ta có:
\(\left\{{}\begin{matrix}3.\left(-2\right)^2+\left(-2\right)b+c=1\\3.4^2+4b+c=7\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}-2b+c=-11\\4b+c=-41\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}b=-5\\c=-21\end{matrix}\right.\)
\(\Rightarrow y=x^2-5x-21\)

a, Bảng biến thiên:
Đồ thị hàm số:
b, Phương trình hoành độ giao điểm
\(-x^2+2x+3=4x-5\)
\(\Leftrightarrow x^2+2x-8=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=2\\x=-4\end{matrix}\right.\)
Nếu \(x=2\Rightarrow y=3\Rightarrow\left(2;3\right)\)
Nếu \(x=-4\Rightarrow y=-21\Rightarrow\left(-4;-21\right)\)
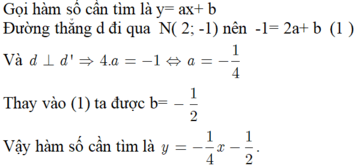

Đáp án D