Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\overrightarrow{a}.\overrightarrow{b}=\left|\overrightarrow{a}\right|.\left|\overrightarrow{b}\right|.cos\left(\overrightarrow{a};\overrightarrow{b}\right)\)
a/ \(\overrightarrow{a}.\overrightarrow{b}=8.\sqrt{3}.cos30^0=12\)
b/ \(\overrightarrow{a}.\overrightarrow{b}=\sqrt{2}.6.cos45^0=6\)
c/ \(\overrightarrow{a}.\overrightarrow{b}=9.10.cos60^0=45\)
d/ \(\overrightarrow{a}.\overrightarrow{b}=5.6.cos120^0=-15\)

a → . b → = a → . b → . c o s a → , b → ⇒ c o s a → , b → = a → . b → a → . b → = − 3 3.2 = − 1 2 ⇒ a → , b → = 120 0 .
Đáp án D

Ta có a → . b → = a → . b → . c o s a → , b → .
⇒ c o s a → , b → = a → . b → a → . b → = − 3 3.2 = − 1 2 ⇒ a → , b → = 120 0
Chọn D.

Ta có: cos a → ; b → = c os 60 0 ⇔ a → . b → a → . b → = 1. 3 + m .1 1 2 + m 2 . 3 + 1 2 = 1 2
⇔ 3 + m 1 + m 2 . 2 = 1 2 ⇔ 3 + m 1 + m 2 = 1 ⇔ 3 + m = 1 + m 2 ⇔ 3 + 2 3 m + m 2 = 1 + m 2 ⇔ 2 3 m = − 2 ⇔ m = − 3 3
Chọn C.

cos a → , b → = a → . b → a → . b → = 3.1 + − 1 .2 3 2 + − 1 2 . 1 2 + 2 2 = 2 10
Chọn A

Ta có a → . b → = a → . b → . c o s a → , b → .
Mà theo giả thiết a → . b → = − a → . b →
Suy ra cos a → , b → = − 1 ⇒ a → , b → = 180 0 .
Chọn A.

Áp dụng hệ quả của định lí cosin ta có
chào tôi tên trợ học lớp 7
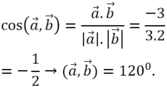
a → = 1 2 + 3 2 = 2 , b → = − 2 3 2 + 6 2 = 48 = 4 3
a → . b → = 1. − 2 3 + 3 .6 = 4 3
cos a → , b → = a → . b → a → b → = 4 3 2.4 3 = 1 2 ⇒ a → , b → = 60
Chọn D