Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

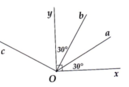
Ta có: a O b ^ = 30°= x O a ^ suy ra
Oa là phân giác của b O x ^ .
Lại có a O y ^ = 60°, Oy là phân
giác của a O c ^ nên:
y O c ^ = a O y ^ = 60°.
Khi. đó:
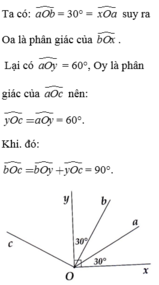
b O c ^ = b O y ^ + y O c ^ = 90°.

a/
Ta có : Góc AOB = Góc xOy - góc AOx - góc bOy = 90o - 30o - 30o =30 o
=> Góc AOB = Góc AOx = 30 o
=> Tia OA là tia phân giác của góc BOx
Vậy tia OA là tia phân giác của góc BOx
b/ Do Oy là phân giác của góc AOC mà góc AOC = Góc AOB + góc BOy = 60o
=> Góc COy = Góc AOC=60o
Góc AON = Góc MON - góc AOM =120o - 90o =30o
Góc BON = Góc MON - Góc BON=120o - 90o =30o
=> Góc AON= Góc BOM
Góc xOy = Góc MON - Góc NOx -Góc MOy = Góc MON - góc AON/2- góc BOM/2 = 120o -30o/2 -30o/2 =90o
=> Ox vuông góc với Oy.
=> Góc BOC = Góc BOy + Góc BON = 60o + 30o =90o
=> OB vuông góc với tia OC.

góc xOB=90o-góc BOy
góc BOx=900-300=600
góc AOB=góc BOx-góc AOx
góc AOB = 60o-30o=30o
mà góc AOB=góc AOx=300
=> OA là phân giác của góc BOx

a) Vì tia OB nằn giữa 2 tia Ox và Oy => góc yOB + BOx = 90o
=> BOx = 90o - yOB = 90o - 30o = 60o
Trên nửa mp bờ tia Ox: góc xOA < xOB (30o < 60o)
=> tia OA nằm giữa 2 tia Ox và OB
=> BOA + AOx = BOx
=> góc BOA = BOx - AOx = 60o - 30o = 30o
Vậy BOA = AOx và OA nằm giữa 2 tia OB và Ox => OA là tia p/g của góc xOB
b) Góc xOA + AOy = xOy
=> AOy = xOy - xOA = 90o - 30o = 60o
Oy là p/g của góc AOC => góc AOC = 2 . góc AOy = 120 o
Trên nửa mp bờ tia OA: góc AOB < góc AOC
=> tia OB nằm giữa 2 tia OA và OC
=> AOB + BOC= AOC
=> BOC = AOC - AOB = 120o - 30o = 90o
=> OB vuông góc với OC

a) Ta có : góc BOA = 900 - yOB - AOx
=) BOA = 900 - 300
=) BOA = 300
vì BOA = AOx = 300
=) OA là tia phân giác của góc BOx
b) Ta có : AOy = 900 - 300 = 600
Vì Oy là tia phân giác của Góc COA
=) Coy = yOA = 600
Vì COy là tia phân giác của góc COA
a,Do \(\widehat{yOB}\)<\(\widehat{yOx}\)và tia OB nằm trong góc \(\widehat{xOy}\)
\(\Rightarrow\)Tia OB nằm giữa hai tia Ox,Oy
\(\Rightarrow\)\(\Rightarrow\widehat{yOB}\)+\(\widehat{BOx}\)=\(\widehat{xOy}\)
\(\Rightarrow30^o+\widehat{BOx}\)\(=90^o\)
\(\Rightarrow\widehat{BOx}\)\(=60^o\)
Do \(\widehat{xOA}\)<\(\widehat{xOB}\)và hai tia OA,OB cùng nằm trong \(\widehat{xOy}\)
\(\Rightarrow\widehat{xOA}+\widehat{AOB}=\widehat{xOB}\)
\(\Rightarrow30^o+\widehat{AOB}=60^o\)
\(\Rightarrow\widehat{AOB}=30^o\)
Do \(\widehat{xOA}=\widehat{AOB}\)\(=\frac{\widehat{BOx}}{2}=\frac{60^o}{2}=30^o\)
\(\Rightarrow\)Tia OA là tia phân giác của \(\widehat{xOB}\)
b, mk chịu