Cho hai mặt cầu ( S 1 ) , S 2 có cùng bán kính R=3 thỏa mãn tính chất tâm của S 1 thuộc S 2 và ngược lại. Tí...

Cho hai mặt cầu ( S 1 ) , S 2 có cùng bán kính R=3 thỏa mãn tính chất tâm...

LV

Lê vsbzhsjskskskssm

18 tháng 8 2021

Cho mặt cầu (S) có tâm O và bán kính R biết diện tích của (S) là 36π. Hai điểm A,B thuộc (S) và khoảng cách từ O đến AB là 2 căn 2 Tính AB

#Toán lớp 12

1

NV

Nguyễn Việt Lâm

Giáo viên

18 tháng 8 2021

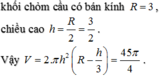
\(S=4\pi R^2=36\pi\Rightarrow R=3\) \(\Rightarrow OA=3\)

Gọi H là trung điểm AB \(\Rightarrow OH\perp AB\) và \(OH=2\sqrt{2}\)

Pitago tam giác vuông OAH:

\(AH=\sqrt{OA^2-OH^2}=1\)

\(\Rightarrow AB=2AH=2\)

Đúng(0)

PT

Pham Trong Bach

14 tháng 4 2019

Cho mặt cầu (S) tâm O, bán kính R = 3. Mặt phẳng (P) cách O một khoảng bằng 1 và cắt (S ) theo giao tuyến là đường tròn (C) có tâm H . Gọi T là giao điểm của tia OH và (S) , tính thể tích V của khối nón có đỉnhT và đáy là hình tròn (C ). ...

Đọc tiếp

#Toán lớp 12

1

CM

Cao Minh Tâm

14 tháng 4 2019

Đáp án C

Đúng(0)

PT

Pham Trong Bach

30 tháng 3 2019

Khi cắt mặt cầu S (O, R) bởi một mặt kính đi qua tâm O, ta được hai nửa mặt cầu giống nhau. Giao tuyến của mặt kính đó với mặt cầu gọi là mặt đáy của mỗi nửa mặt cầu. Một hình trụ gọi là nội tiếp nửa mặt cầu S (O, R) nếu một đáy của hình trụ nằm trong đáy của nửa mặt cầu, còn đường tròn đáy kia là giao tuyến của hình trụ với nửa mặt cầu. Biết R = 1, tính bán kính...

Đọc tiếp

#Toán lớp 12

1

CM

Cao Minh Tâm

30 tháng 3 2019

Đúng(0)

PT

Pham Trong Bach

20 tháng 11 2017

Trong không gian với hệ tọa độ Oxyz, cho hai điểm A (0; 2; 2), B (2; -2; 0). Gọi I1 (1; 1; -1) và I2 (3; 1; 1) là tâm của hai đường tròn nằm trên hai mặt phẳng khác nhau và có chung một dây cung AB. Biết rằng luôn có một mặt cầu (S) đi qua cả hai đường tròn ấy. Tính bán kính R của (S). A . R = 219 3 B. R = 2 2 C . R = 129 3 D. R = 2 6 ...

Đọc tiếp

#Toán lớp 12

1

CM

Cao Minh Tâm

20 tháng 11 2017

Chọn C

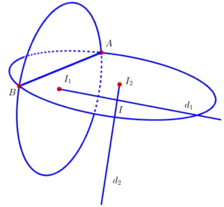
Gọi d₁ là đường thẳng đi qua I₁ và vuông góc với mặt phẳng (ABI₁), khi đó d₁ chứa tâm các mặt cầu đi qua đường tròn tâm I₁; d₂ là đường thẳng đi qua I₂ và vuông góc với mặt phẳng (ABI₂), khi đó d₂ chứa tâm các mặt cầu đi qua đường tròn tâm I₂.