Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

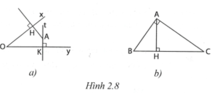
Trên hình 2.8a) có A H ⊥ O x , A K ⊥ O y nên các góc có cạnh tương ứng vuông góc là: góc HAK và góc xOy; góc HAt và góc xOy.
Trên hình 2.8b) có A B ⊥ A C ; A H ⊥ B C và nên các góc có cạnh tương ứng vuông góc là: góc BAH và góc C; góc CAH và góc B.

Giải
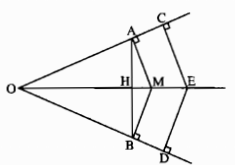
a) Gọi H là giao điểm của AB và OM. Xét hai tam giác vuông AOM và BOM. Ta có cạnh huyền OM chung, MA = MB (vì M thuộc tia phân giác của góc O). Vậy ∆AOM = ∆BOM. Suy ra OA = OB. Từ đó có ∆AOH = ∆BOH (c.g.c). Suy ra ˆAHO=ˆAHB=90∘AHO^=AHB^=90∘, tức là OM⊥ABOM⊥AB
b) Để chứng minh OE là tia phân giác của góc O, ta cần chứng minh hai tam giác vuông COE và DOE bằng nhau. Hai tam giác này có cạnh huyền OE chung và OC = OD (giả thiết) nên chúng bằng nhau. Suy ra ˆEOC=ˆEODEOC^=EOD^ hay OE là tia phân giác của góc O.

a) Gọi H là giao điểm của AB và OM. Xét hai tam giác vuông AOM và BOM. Ta có cạnh huyền OM chung, MA = MB (vì M thuộc tia phân giác của góc O). Vậy ∆AOM = ∆BOM. Suy ra OA = OB. Từ đó có ∆AOH = ∆BOH (c.g.c). Suy ra ˆAHO=ˆAHB=90∘AHO^=AHB^=90∘, tức là OM⊥ABOM⊥AB
b) Để chứng minh OE là tia phân giác của góc O, ta cần chứng minh hai tam giác vuông COE và DOE bằng nhau. Hai tam giác này có cạnh huyền OE chung và OC = OD (giả thiết) nên chúng bằng nhau. Suy ra ˆEOC=ˆEODEOC^=EOD^ hay OE là tia phân giác của góc O.

Câu hỏi của le thu giang - Toán lớp 7 - Học toán với OnlineMath
Em tham khảo bài làm tương tự ở link trên.
a) (+) Nếu hai góc kề bù AMB và BMC bằng nhau thì ta có:
\(\widehat{AMB}=\widehat{BMC}=\dfrac{180^o}{2}=90^o\)
Vậy khi hai góc bằng nhau thì ta có: \(\widehat{AMB}=\widehat{BMC}=90^o\)
(+) Nếu giả sử góc AMB lớn gấp hai lần góc BMC thì ta có:
\(1\widehat{AMB}=2\widehat{BMC}\left(\widehat{AMB}+\widehat{BMC}=180^o\right)\)
\(\Rightarrow\widehat{AMB}=180:3.2=120^o\)
\(\Rightarrow\widehat{BMC}=180^o-120^o=60^o\)
Vậy khi góc AMB lớn gấp đôi góc BMC thì \(\widehat{AMB}=120^o\)
\(\widehat{BMC}=60^o\)
Nếu điều giả sử ngược lại thì kết quả cũng ngược lại
b) 2 đường thẳng nhé