Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

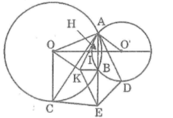
Vì AB ⊥ KB nên AE ⊥ KB
Lại có: AB = BE (tính chất đối xứng tâm)
Suy ra: KA = KE (tính chất đường trung trực) (3)
Ta có: IO = IO’ (gt)
IA = IK (chứng minh trên)
Tứ giác AOKO’ có hai đường chéo cắt nhau tại trung điểm của mỗi đường nên nó là hình bình hành
Suy ra: OK // O’A và OA // O’K
CA ⊥ O’A (vì CA là tiếp tuyến của đường tròn (O’))
OK // O’A (chứng minh trên)
Suy ra: OK ⊥ AC
Khi đó OK là đường trung trực của AC
Suy ra: KA = KC (tính chất đường trung trực) (4)
DA ⊥ OA (vì DA là tiếp tuyến của đường tròn (O))
O’K // OA (chứng minh trên)
Suy ra: O’K ⊥ DA
Khi đó O’K là đường trung trực của AD
Suy ra: KA = KD (tính chất đường trung trực) (5)
Từ (3), (4) và (5) suy ra: KA = KC = KE = KD
Vậy bốn điểm A, C, E, D cùng nằm trên một đường tròn.3

a: Xét tứ giác OBAC có
\(\widehat{OBA}+\widehat{OCA}=180^0\)
Do đó: OBAC là tứ giác nội tiếp
hay A,B,O,C cùng thuộc 1 đường tròn

a: OH*OM=OA^2=R^2
b: ΔOCD cân tại O
mà OI là đường trung tuyến
nên OI vuông góc với CD
Xét tứ giác OIAM có
góc OIM=góc OAM=90 độ
nên OIAM là tứ giác nội tiếp
c: Xét ΔOHK vuông tại H và ΔOIM vuông tại I có
góc HOK chung
Do đo: ΔOHK đồng dạng với ΔOIM
=>OH/OI=OK/OM
=>OI*OK=OH*OM=R^2=OC^2
mà CI vuông góc với OK
nên ΔOCK vuông tại C
=>KC là tiếp tuyến của (O)

Cho đường tròn (O), đường kính AB. Trên tiếp tuyến của (O) tại A lấy điểm M (M khác A). Từ M kẻ cát tuyến MCD (C nằm ở giữa M và D; tia MC nằm giữa MA và MO) và tiếp tuyến thứ hai MI (I là tiếp điểm) với đường tròn (O). Đường thẳng BC và BD cắt đường thẳng OM lần lượt tại E và F. Chứng minh:
O là trung điểm của EF
a: OH*OA=OB^2=R^2
b: ΔOCD cân tại O
mà OM là trung tuyến
nên OM vuông góc với CD
Xét tứ giác OMBA có
góc OMA=góc OBA=90 độ
nên OMBA là tứ giác nội tiếp
c: Xét ΔOHE vuông tại H và ΔOMA vuông tại M có
góc MOA chung
Do đó: ΔOHE đồng dạng với ΔOMA
=>OH/OM=OE/OA
=>OM*OE=OH*OA=R^2=OC^2=OD^2
=>ΔODE vuông tại D
=>DE là tiếp tuyến của (O)
