Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

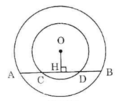
Giả sử vị trí các điểm theo thứ tự là A, C, B, D.
Kẻ OH ⊥ CD. Theo tính chất đường kính vuông góc với một dây ta có:
HA = HB, HC = HD
Nên AC = HA – HC = HB – HD = BD
Vậy AC = BD.
(Trường hợp vị trí các điểm theo thứ tự là A, D, C, B chứng minh tương tự.)

Nguyễn Duy Khánh
Vẽ .

Theo tính chất đường kính vuông góc với một dây ta được MA=MB và MC=MD.
Từ đó suy ra AC=BD.
Nhận xét. Kết luận bài toán vẫn được giữ nguyên nếu C và D đổi chỗ cho nhau.
Ai k mình và kết bạn với mình mình sẽ trả ơn .

Vẽ OM⊥AB⇒OM⊥CD.
Xét đường tròn (O;OC) (đường tròn nhỏ) có OM là một phần đường kính, CD là dây và OM⊥CD nên M là trung điểm của CD hay MC=MD (định lý)
Xét đường tròn (O;OA) (đường tròn lớn) có OM là một phần đường kính, AB là dây và OM⊥AB nên M là trung điểm của AB hay MA=MB (định lý)
Ta có MA=MB và MC=MD (cmt) nên trừ các đoạn thẳng theo vế với vế ta được MA−MC=MB−MD ⇒AC=BD.
Nhận xét. Kết luận bài toán vẫn được giữ nguyên nếu C và D đổi chỗ cho nhau.

Hướng dẫn giải:
Vẽ OM⊥ABOM⊥AB.

Theo tính chất đường kính vuông góc với một dây ta được MA=MB và MC=MD.
Từ đó suy ra AC=BD.
Nhận xét. Kết luận bài toán vẫn được giữ nguyên nếu C và D đổi chỗ cho nhau.

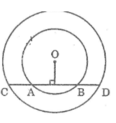
Kẻ OI ⊥ AB. Ta có: OI ⊥ CD
Trong đường tròn (O) (nhỏ) ta có : OI ⊥ AB
Suy ra :
IA = IB (đường kính vuông góc dây cung) (1)
Trong đường tròn (O) (lớn) ta có : OI ⊥ CD
Suy ra :
IC = ID (đường kính vuông góc dây cung)
Hay IA + AC = IB + BD (2)
Từ (1) và (2) suy ra: AC = BD.

* Xét tam giác ACO có CO’ là đường trung tuyến và 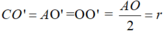
Suy ra, tam giác ACO vuông tại C
⇒ AC ⊥ CO
* Xét tam giác AOD có AO = OD = R
Suy ra tam giác AOD cân tại O.
Lại có OC là đường cao nên đồng thời là đường trung tuyến
⇒ C là trung điểm AD hay AC = CD. (điều phải chứng minh)

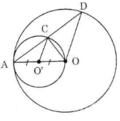
a) Gọi O’ là tâm của đường tròn đường kính OA.
Gọi R và r lần lượt là bán kính đường tròn tâm O và tâm O’.

Suy ra, hai đường tròn đã cho tiếp xúc trong với nhau.
b) +) Xét đường tròn (O’) có A, O, C là ba điểm cùng thuộc đường tròn và OA là đường kính nên tam giác AOC vuông tại C.
⇒ OC ⊥ AD
+) Xét đường tròn tâm (O) có A, D là hai điểm thuộc đường tròn nên OA = OD
⇒ ΔAOD cân tại O mà OC ⊥ AD
⇒ OC là đường trung tuyến của ΔAOD
⇒ C là trung điểm của AD
⇒ AC = CD
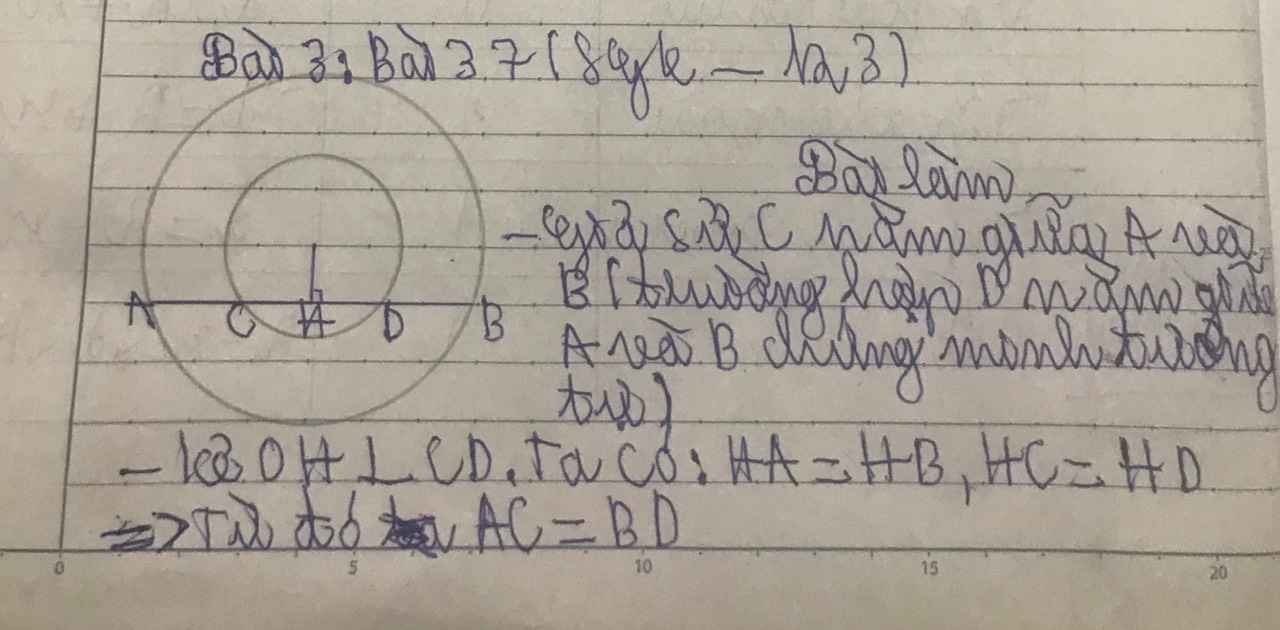
Giả sử vị trí các điểm theo thứ tự là A, C, B, D.
Kẻ OH ⊥ CD. Theo tính chất đường kính vuông góc với một dây ta có:
HA = HB, HC = HD
Nên AC = HA – HC = HB – HD = BD
Vậy AC = BD.
(Trường hợp vị trí các điểm theo thứ tự là A, D, C, B chứng minh tương tự.)