Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có: Oz là tia phân giác của \(\widehat{xOy}\) (gt)
\(\Rightarrow\widehat{xOz}=\widehat{yOz}\)
Vì \(Oz\perp Oz'\) (gt) nên: \(\widehat{yOz}+\widehat{yOz'}=90^o\)
Lại có: \(\widehat{xOz}+\widehat{yOz}+\widehat{yOz'}+\widehat{x'Oz'}=180^o\)
\(\Rightarrow\widehat{xOz}+\widehat{x'Oz'}=180^o-\left(\widehat{yOz}+\widehat{yOz'}\right)\)
\(=180^o-90^o=90^o\)
\(\Rightarrow\widehat{xOz}+\widehat{x'Oz'}=\widehat{yOz}+\widehat{yOz'}=90^o\)
Mà \(\widehat{xOz}=\widehat{yOz}\) (cmt)
\(\Rightarrow\widehat{x'Oz'}=\widehat{yOz'}\)
`=>` Tia Oz' là tia phân giác của \(\widehat{x'Oy}\) (đpcm)

Ta có: \(\widehat{xOz}=\dfrac{\widehat{xOy}}{2}=\dfrac{30^0}{2}=15^0\)
\(\Leftrightarrow\widehat{zOx'}=180^0-15^0=165^0\)

1) Ta có: Oz nằm giữa tia Ox và Oy
\(\Rightarrow\widehat{xOz}=\widehat{xOy}-\widehat{yOz}=120^0-30^0=90^0\)
=> Oz⊥Ox
2) Ta có: Ox' là tia đối của tia Ox
\(\Rightarrow\widehat{x'Oy}=180^0-\widehat{xOy}=180^0-120^0=60^0\)(2 góc kề bù)
Ta có: Ox' là tia đối của tia Ox, Oy' là tia đối của tia Oy
\(\widehat{\Rightarrow x'Oy'}=\widehat{xOy}=120^0\)(2 góc đối đỉnh)
1: Trên cùng một nửa mặt phẳng bờ chứa tia Oy, ta có: \(\widehat{yOz}< \widehat{yOx}\)
nên tia Oz nằm giữa hai tia Ox và Oy
Suy ra: \(\widehat{xOz}+\widehat{yOz}=\widehat{xOy}\)
\(\Leftrightarrow\widehat{xOz}=90^0\)
hay Ox\(\perp\)Oz

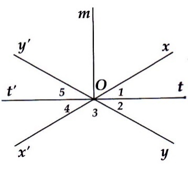
a) Ta có: \(\widehat{O_1}=\dfrac{\widehat{xOy}}{2}\)
Mà \(\widehat{O_1}=\widehat{O_2}\) ( đối đỉnh )
\(\widehat{xOy}=\widehat{x'Oy'}\) ( đối đỉnh )
\(\widehat{O_4}=\widehat{O_5}\)
Lại có:
\(\widehat{xOt'}=\widehat{xOy'}\) \(+\) \(\widehat{O_5}\) và \(\widehat{t'Oy}=\widehat{x'Oy}\) \(+\) \(\widehat{O_4}\)
Mà \(\widehat{xOy'}=\widehat{x'Oy}\) ( đối đỉnh )
\(\widehat{O_4}=\widehat{O_5}\)
⇒ \(\widehat{xOt'}=\widehat{tOy'}\) ( đpcm )
b) Vì \(\widehat{xOm}=\dfrac{1}{2}\widehat{xOy'}\) ; \(\widehat{O_1}=\dfrac{1}{2}\widehat{xOy}\) nên
\(\widehat{mOt}=\widehat{xOm}\) \(+\) \(\widehat{O_1}\) \(=\) \(\dfrac{1}{2}\left(\widehat{xOy'}+\widehat{xOy}\right)=90^o\)
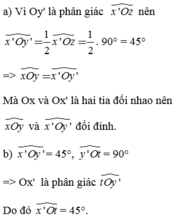
Mk cần gấp ạ :<<<