Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Xét đường thẳng d qua M và d ⊥ (α).
Khi đó H chính là giao điểm của d và (α).
Vectơ (1 ; 1 ; 1) là vectơ pháp tuyến của (α) nên
là vectơ chỉ phương của d.
Phương trình tham số của đường thẳng d có dạng: .
Thay tọa độ x ; y ; z của phương trình trên vào phương trình xác định (α), ta có:
3t + 6 = 0 => t = -2 => H(-1 ; 2 ; 0).
b) Gọi M'(x ; y ; z) là điểm đối xứng của M qua mặt phẳng (α), thì hình chiếu vuông góc H của M xuống (α) chính là trung điểm của MM'.
Ta có:
=> x = -3 ;
=> y = 0 ;
=> z = -2.
Vậy M'(-3 ; 0 ;2).
c) Tính khoảng cách từ điểm M đến mặt phẳng (α) bằng 2 cách sau:
Cách 1: Áp dụng công thức ta có:
.
Cách 2: Khoảng cách từ M đến (α) chính là khoảng cách MH:
d(M,(α) )= MH = .

a) Xét đường thẳng d qua M và d ⊥ (α).
Khi đó H chính là giao điểm của d và (α).
Vectơ (1 ; 1 ; 1) là vectơ pháp tuyến của (α) nên
là vectơ chỉ phương của d.
Phương trình tham số của đường thẳng d có dạng: .
Thay tọa độ x ; y ; z của phương trình trên vào phương trình xác định (α), ta có:
3t + 6 = 0 => t = -2 => H(-1 ; 2 ; 0).
b) Gọi M'(x ; y ; z) là điểm đối xứng của M qua mặt phẳng (α), thì hình chiếu vuông góc H của M xuống (α) chính là trung điểm của MM'.
Ta có:
=> x = -3 ;
=> y = 0 ;
=> z = -2.
Vậy M'(-3 ; 0 ;2).
c) Tính khoảng cách từ điểm M đến mặt phẳng (α) bằng 2 cách sau:
Cách 1: Áp dụng công thức ta có:
.
Cách 2: Khoảng cách từ M đến (α) chính là khoảng cách MH:
d(M,(α) )= MH = .

Chọn đáp án C
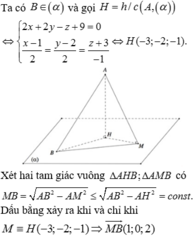
Mặt cầu (S) có tâm I(4;3;3) và bán kính R = 4. Gọi I’ là hình chiếu của I trên mặt phẳng α .
Đường thẳng I I ' đi qua I(4;3;3) và nhận n = ⇀ 1 ; 1 ; 1 làm vectơ chỉ phương nên có phương trình là:
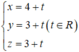
Tọa độ điểm I’ thỏa mãn hệ
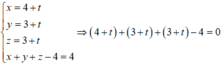
⇔ t = - 2 . Suy ra I’(2;1;1).
Gọi hình tròn (C) bán kính r là thiết diện của khối cầu (S) khi cắt bởi mặt phẳng α . Khi đó I’ là tâm của đường tròn (C).
Ta có I M = 14 < 4 = R và M ∈ α nên điểm M thuộc miền trong của đường tròn (C) (M nằm trong hình trong hình tròn).
Do đường thẳng d ⊂ α , d đi qua M và d cắt mặt cầu tại hai điểm A, B nên d cắt đường tròn (C) tại hai điểm A, B.
Phương tích của điểm M với đường tròn (C): M A . M B = r 2 - I ' M 2 .
Do r không đổi nên r 2 - I ' M 2 không đổi ⇒ M A . M B không đổi.
Lại có
![]()
Dấu “=” xảy ra khi MA = MB hay A B ⊥ M I ' .
Mà A B ⊥ M I ' nên đường thẳng AB có một vectơ chỉ phương là u ⇀ = I I ' ; ⇀ M I ' ⇀ = 2 ; - 4 ; 2 (cùng phương với vectơ u 2 ⇀ )

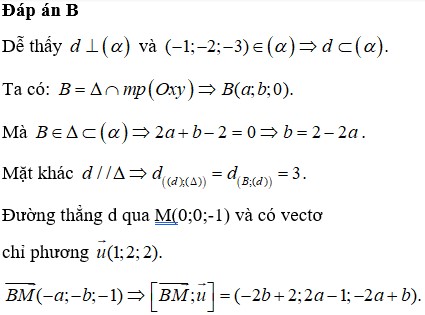
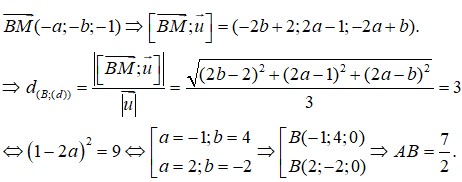

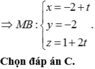

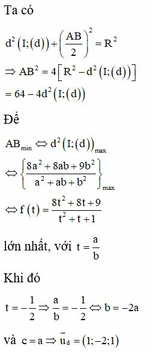

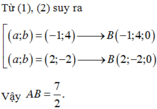
Đáp án D
Ta có f = 3 x - y + z - 2 ⇒ f A . f B = 1 . 8 = 8 > 0 ⇒ A, B nằm về hai phía đối với α .