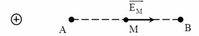Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Giả sử điện tích q đặt tại O như hình vẽ:
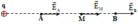
Ta có: E A = k q ε . O A 2 ; E B = k q ε . O B 2 ; E M = k q ε . O M 2
Vì M là trung điểm AB nên O M = O A + O B 2
Thay OA, OB, OM vào biểu thức trên ta được:
1 E M = 1 2 1 E A + 1 E B → E M = 4 E A E B E A + E B 2 = 16 V / m

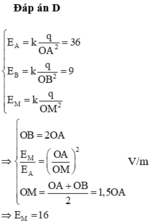
\(E_A=\dfrac{kq}{r_A^2}=36;E_B=\dfrac{kq}{\left(r_A+AB\right)^2}=9\)
\(\Rightarrow\dfrac{E_A}{E_B}=\dfrac{\left(r_A+AB\right)^2}{r^2_A}=4\Leftrightarrow r_A+AB=2r_A\Leftrightarrow r_A=AB\)
\(E_M=\dfrac{kq}{\left(r_A+\dfrac{AB}{3}\right)^2}=\dfrac{kq}{\left(\dfrac{4}{3}r_A\right)^2}=\dfrac{9}{16}.E_A=...\left(V/m\right)\)

a) Các điện tích q 1 v à q 2 gây ra tại M các véc tơ cường độ điện trường E 1 → và E 2 → có phương chiều như hình vẽ.
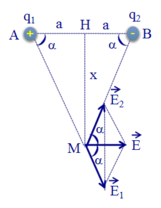
Có độ lớn: E 1 = E 2 = k q ε ( a 2 + x 2 )
Cường độ điện trường tổng hợp tại M do các điện tích q 1 v à q 2 gây ra là:
E → = E 1 → + E 2 → ; có phương chiều như hình vẽ.
Có độ lớn: 2 E 1 cos α = 2 . k q ( a 2 + x 2 ) a a 2 + x 2 = 2 k q a ( a 2 + x 2 ) 3 2
b) Theo câu a ta có: E = 2 k q a ( a 2 + x 2 ) 3 2 ; để E có giá trị cực đại thì mẫu số phải có giá trị cực tiểu mà mẫu số có giá trị cực tiểu khi x = 0 tức là M trùng với H.

a) Các điện tích q1 và q2 gây ra tại M các véc tơ cường độ điện trường E 1 → và E 2 → có phương chiều như hình vẽ:

Có độ lớn: E 1 = E 2 = k q ( a 2 + x 2 ) .
Cường độ điện trường tổng hợp tại M do các điện tích q 1 v à q 2 gây ra là:
E → = E 1 → + E 2 → ; có phương chiều như hình vẽ.
Có độ lớn: E = E 1 cos α + E 2 cos α = 2 E 1 cos α = 2 . k q ( a 2 + x 2 ) . x a 2 + x 2 = 2 k q x ( a 2 + x 2 ) 3 2
b) Theo câu a ta có E = 2 k q x ( a 2 + x 2 ) 3 2 = 2 k q a 2 x 2 3 + x 4 3 3 2 .
Để E có giá trị cực đại thì mẫu số phải có giá trị cực tiểu mà mẫu số có giá trị cực tiểu khi a 2 x 2 3 = x 4 3 (theo bất đẳng thức Côsi) ð a 2 = x 2 hay x = a.