Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Phương pháp: Sử dụng định luật bảo toàn cơ năng
Cách giải: Theo đề biên độ của con lắc thứ nhất và thứ hai lần lượt là: nA, A
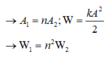
Mặt khác hai dao động cùng pha nên W t 1 = n 2 W t 2
* Khi động năng của con lắc thứ nhất là a thì thế năng của con lắc thứ hai là b suy ra:
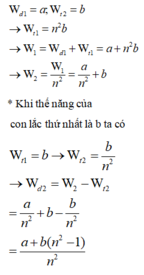
Đáp án A
Đáp án C
Cơ năng của vật 1 và vật 2:
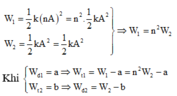
Hai dao động cùng pha nên ngoài vị trí biên và VTCB ta có: W d 1 W d 2 = W t 1 W t 2 = W 1 W 2 = n 2
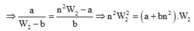
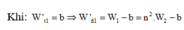
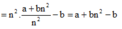
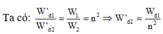
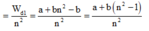
Đáp án D
Vì hai dao động là luôn cùng pha nên ta có: x 1 x 2 2 = E t 1 E t 2 = A 1 A 2 2 ↔ x 1 x 2 2 = E t 1 E t 2 = A 1 A 2 2 → E 1 = 2 , 88 J → E 2 = 0 , 32 J
Vì hai dao động là luôn cùng pha nên ta có:
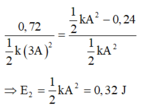
Khi thế năng của con lắc thứ nhất là 0,09 J thì:
Đáp án D
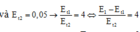
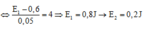
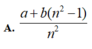
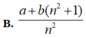
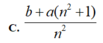
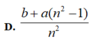
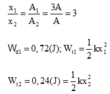
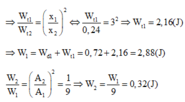
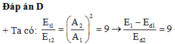
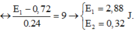
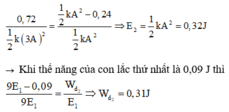
Chọn B
+ Do hai con lắc giống hệt nhau nên chúng có cùng khối lượng m và độ cứng k.
+ Xét tỉ số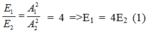
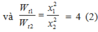do x1 = 2A cos(ωt); x2 = Acos(ωt).
+ Khi Wt2 = 0,05J => Wt1 = 0,2J do (2) => E1 = Wt1 + Wđ1 = 0,2 + 0,6 = 0,8J => E2 = 0,2J.
+ Khi Wt1’ = 0,4J = Wt2’ = 0,1J. Lại có E2 = 0,2J = Wt2’ + Wđ2 =>Wđ2’= 0,1J.