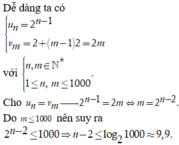Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B
a n là cấp số cộng có công sai d = 3 ⇒ a n = 4 + 3 n − 1 là số hạng tổng quát của b n
b n là cấp số cộng có công sai d = 5 ⇒ b n = 1 + 5 n − 1 là số hạng tổng quát của b n
Suy ra a n = b n ⇔ 4 + 3 n 1 − 1 = 1 + 5 n 2 − 1 ⇔ 5 n 2 − 3 n 1 = 5
Suy ra 3 n 1 ⋮ 5 , đặt 3 n 1 = 5 x ⇒ x ⋮ 3 ⇒ 5 n 2 = 5 x = 5 ⇔ n 2 − x = 1
1 ≤ n 1 ≤ 100 ⇒ 3 5 ≤ x ≤ 60 , x ⋮ 3 , x ∈ ℕ ⇒ có 60 − 3 3 + 1 = 20 giá trị x thỏa mãn.
Suy ra có 20 số xuất hiện trọng cả hai dãy số trên

Đáp án C.
Phương pháp
Sử dụng công thức số hạng tổng quát của CSC: u n = u 1 + n − 1 d
Cách giải
Ta có
u n = 1 + 5 n − 1 = 5 n − 4 0 ≤ n ≤ 2018 , n ∈ ℤ v m = 4 + 3 m − 1 = 3 m + 1 0 ≤ m ≤ 2018 , m ∈ ℤ u n = v m ⇔ 5 n − 4 = 3 m + 1 ⇔ n = 3 m + 5 5 = 3 m 5 + 1 ⇒ m ⋮ 5 ; 0 ≤ m ≤ 2018 ⇒ m = 5 k k ∈ ℤ ; 0 ≤ 5 k ≤ 2018 ⇒ 0 ≤ k ≤ 403
Có 403 giá trị của n thỏa mãn

Đáp án D
Các dãy số (hữu hạn hoặc vô hạn) với số hạng tổng quát có dạng an+b ( a, b là hằng số) đều là một cấp số cộng với công sai d = a


4a.
Số tự nhiên là A, ta có:
A = 7m + 5
A = 13n + 4
=>
A + 9 = 7m + 14 = 7(m + 2)
A + 9 = 13n + 13 = 13(n+1)
vậy A + 9 là bội số chung của 7 và 13
=> A + 9 = k.7.13 = 91k
<=> A = 91k - 9 = 91(k-1) + 82
vậy A chia cho 91 dư 82
4b.
Giả sử p là 1 số nguyên tố >3, do p không chia hết cho 3 nên p có dạng 3k + 1 hoặc 3k + 2
Vì p +4 là số nguyên tố nên p không thể có dạng 3k + 2
Vậy p có dạng 3k +1.
=> p + 8 = 3k + 9 chia hết cho 3 nên nó là hợp số.