Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

hình bn tự vẽ nhé:
a/ Vì đường thẳng zz' vuông góc với Ox tại O nên
xOz=90*
Vì xOy > xOz ( 135*> 90*)
=> Oz nằm giữa 2 tia Ox và Oy
Ta có: xOz + zoy = xoy
90*+ zoy = 135*
=> zoy= 45*
Vì tt' vuông góc với Oy tại O nên
yot = 90*
Vì toy> zoy( 90*>45*)
=> Oz nằm giữa 2 tia Oy và Ot
Ta có: zOy + zOt = tOy
45* + zOt = 90*
=> zOt= 45*
Vì Oz nằm giữa 2 tia Ot và Oy
zOy=zOt=45*
=> Oz là tia phân giác của tOy
b/ Vì x'Ot' đối đỉnh với tOx
=> x'Ot'=45*
Vì xOy' đối đỉnh với yOx'
=> xOy'=45*
Vì x'Ot'=xOy'=45*
Nên x'Ot' = xOy'
Chúc bn hc tốt nha, các góc kia là bn tự thêm dấu mũ vào nhé

![]() .
.
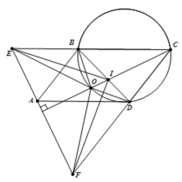
3). Theo trên, ta có B E = C D mà C E = C F ⇒ B C = D F .
Ta có CI là đường phân giác góc BCD, nên I B I D = C B C D = D F B E ⇒ I B . B E = I D . D F .
Mà CO là trung trực EF và I ∈ C O , suy ra IE=IF.
Từ hai đẳng thức trên, suy ra I B . B E . E I = I D . D F . F I .

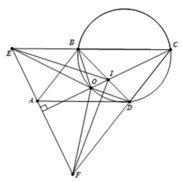
2). Từ Δ O B E = Δ O D C ⇒ O E = O C .
Mà CO là đường cao tam giác cân CEF , suy ra OE=OF.
Từ đó
O
E
=
O
C
=
O
F
, vậy O là tâm đường tròn ngoại tiếp tam giác ![]() .
.

Giải:
Xét \(\Delta AHI,\Delta AKI\) có:
\(\widehat{AHI}=\widehat{AKI}=90^o\)
AI: cạnh chung
\(\widehat{A_1}=\widehat{A_2}\left(=\frac{1}{2}\widehat{A}\right)\)
\(\Rightarrow\Delta AHI=\Delta AKI\) ( c.huyền - g.nhọn )
\(\Rightarrow HI=KI\) ( cạnh t/ứng ) (1)
Xét \(\Delta BHI,\Delta CKI\) có:
IB = IC ( gt )
\(\widehat{BHI}=\widehat{CKI}=90^o\)
IH = IK ( theo (1) )
\(\Rightarrow\Delta BHI=\Delta CKI\) ( c.huyền - c.g.vuông)
\(\Rightarrow BH=CK\) ( cạnh t/ứng ) ( đpcm )
Vậy...

a: Xét ΔOAM vuông tại A và ΔODM vuông tại D có
OM chung
\(\widehat{AOM}=\widehat{DOM}\)
DO đó: ΔOAM=ΔODM
b: Xét ΔMAE vuông tại A và ΔMDB vuông tại D có
MA=MD
\(\widehat{AME}=\widehat{DMB}\)
Do đó: ΔMAE=ΔMDB
c: Ta có: ΔMAE=ΔMDB
nên ME=MD
d: Ta có: ΔOEB cân tại O
mà OM là phân giác
nên OM là đường cao