Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a,b: Xét ΔOAM vuông tại A và ΔOBM vuông tạiB co
OM chung
góc AOM=góc BOM
=>ΔOAM=ΔOBM
=>OA=OB và MA=MB
=>ΔOAB cân tại O
c: Xét ΔMAD vuông tại A và ΔMBE vuông tại B có
MA=MB
góc AMD=góc BME
=>ΔMAD=ΔMBE
=>MD=ME

Em tham khảo tại link dưới đây nhé.
Câu hỏi của trần thị thúy vân - Toán lớp 7 - Học toán với OnlineMath

a. Xét △OAM và △OBM có:
\(\hat{OAM}=\hat{OBM}=90^o\)
\(OM\) chung
\(\hat{AOM}=\hat{BOM}\) (do M thuộc tia phân giác của \(\hat{xOy}\))
\(\Rightarrow\Delta OAM=\Delta OBM\left(c.h-g.n\right)\)
\(\Rightarrow MA=MB\) (đpcm).
b. Từ a. \(\Rightarrow OA=OB\)
⇒ Tam giác OAB cân tại O.
c. Xét △BME và △AMD có:
\(\hat{MBE}=\hat{MAD}=90^o\)
\(MA=MB\left(cmt\right)\)
\(\hat{AMD}=\hat{BME}\) (đối đỉnh)
\(\Rightarrow\Delta BME=\Delta AMD\left(g.n-c.g.v\right)\)
\(\Rightarrow MD=ME\left(đpcm\right)\)
d. Ta có: \(OA=OB\left(cmt\right)\), \(AD=DE\) (suy ra từ c.)
\(\Rightarrow OA+AD=OB+DE\)
\(\Rightarrow OD=OE\)
⇒ Tam giác ODE cân tại O.
Tam giác ODE cân tại O có OM là đường phân giác ⇒ OM cũng là đường cao.
\(\Rightarrow OM\perp DE\left(đpcm\right)\)


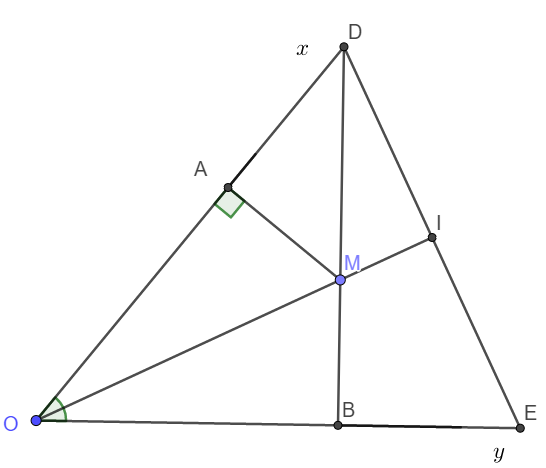
a) Xét tam giác vuông AOM và tam giác vuông BƠM có:
Cạnh huyền AM chung
\(\widehat{AOM}=\widehat{BOM}\) (gt)
\(\Rightarrow\Delta AOM=\Delta BOM\) (Cạnh huyền - góc nhọn)
\(\Rightarrow MA=MB;OA=AB\)hay tam giác OAB cân tại O.
b) Xét tam giác vuông AMD và tam giác vuông BME có:
AM = BM
\(\widehat{AMD}=\widehat{BME}\) (Hai góc đối đỉnh)
\(\Rightarrow\Delta AMD=\Delta BME\) (Cạnh góc vuông - góc nhọn kề)
\(\Rightarrow MD=ME\)
c) Ta thấy OA = OB; AD = BE nên OD = OE
Vậy thì \(\Delta ODI=\Delta OEI\left(c-g-c\right)\)
\(\Rightarrow\widehat{OID}=\widehat{OIE}\)
Chúng lại là hai góc kề bù nên \(\widehat{OID}=\widehat{OIE}=90^o\) hay MO vuông góc DE.
MỌI NGƯỜI ƠI GIÚP E VỚI Ạ EM ĐANG CẦN RẤT GẤP Ạ
viết chữ cũng sai ah đây dell buồn giúp