Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a, Chỉ ra |OI – OK| < IK < OI + OK => (1) và (k) luôn cắt nhau
b, Do OI=NK, OK=IM => OM=ON
Mặt khác OMCN là hình chữ nhật => OMCN là hình vuông
c, Gọi{L} = KB ∩ MC, {P} = IBNC => OKBI là Hình chữ nhật và BNMI là hình vuông
=> ∆BLC = ∆KOI
=> L B C ^ = O K I ^ = B I K ^
mà B I K ^ + I B A ^ = 90 0
L B C ^ + L B I ^ + I B A ^ = 180 0
d, Có OMCN là hình vuông cạnh a cố định
=> C cố định và AB luôn đi qua điểm C

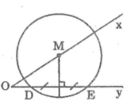
* Cách dựng:
- Dựng đường trung trực của DE cắt Ax tại M
- Dựng đường tròn tâm M bán kính MD
* Chứng minh:
Theo cách dựng ta có: M ∈ Ox
MD = ME (tính chất đường trung trực)
Suy ra: E ∈ (M; MD).

* Phân tích
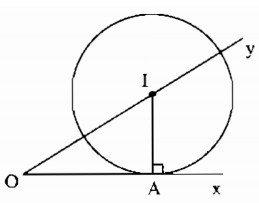
Giả sử đường tròn tâm I dựng được thỏa mãn điều kiện bài toán.
− Đường tròn tâm I tiếp xúc với Ox tại A nên I nằm trên đường thẳng vuông góc với Ox kẻ từ A.
− Tâm I nằm trên tia Oy nên I là giao điểm của Oy và đường thẳng vuông góc với Ox tại A.
* Cách dựng
− Dựng đường vuông góc với Ox tại A cắt Oy tại I.
− Dựng đường tròn (I; IA).
* Chứng minh
Ta có: I thuộc Oy, OA ⊥ IA tại A.
Suy ra Ox là tiếp tuyến của đường tròn ( I;IA)
hay (I; IA) tiếp xúc với Ox.
* Biện luận
Vì góc xOy là góc nhọn nên đường thẳng vuông góc với Ox tại A luôn cắt tia Oy nên tâm I luôn xác định và duy nhất.
Theo đề bài ta có I là trung điểm đoạn EF => I thuộc tia phân giác góc xOy => góc EOI = góc FOI
Cho H,K là chân các đường vuông góc hạ từ M xuống các tia Ox, Oy => \(MH⊥Ox;MK⊥Oy\)(1)
ta có : góc MHO = góc MKO = 900
=> tứ giác OHMK nội tiếp => góc MOK = góc MHK(cùng chắn cung MK),góc MOH = góc HKM (cùng chắn cung HM)
Mà góc MOK = góc MOH (cmt) nên góc MHK = góc HKM => tam giác MHK cân tại M => MH = MK (2)
Từ (1) và (2) => M thuộc đường phân giác của góc xOy
Vì I và M đều thuộc tia phân giác của góc xOy nên I,OM thẳng hàng
p/s còn nhiều cách khác .vd: (dùng hình vẽ trên) : chứng minh 2 tam giác HMO = tam giác KMO( tam giác vuông có cạnh OM chung và góc HOM = góc MOK) => MH=MK -> phần sau làm tương tự.............[cách này ngắn hơn nhưng không dùng cho lớp 9 HKII]
Chưa học