Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

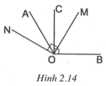 a) Tia OM là tia phân giác của góc AOB nên
A
O
M
^
=
B
O
M
^
=
120
°
:
2
=
60
°
.
a) Tia OM là tia phân giác của góc AOB nên
A
O
M
^
=
B
O
M
^
=
120
°
:
2
=
60
°
.
Ta có O C ⊥ O B ⇒ B O C ^ = 90 ° .
Tia OM nằm giữa hai tia OB, OC nên B O M ^ + C O M ^ = B O C ^
⇒ C O M ^ = 90 ° − 60 ° = 30 °
Tia OC nằm giữa hai tia OA, OB nên A O C ^ + B O C ^ = A O B ^
⇒ A O C ^ = 120 ° − 90 ° = 30 °
Vậy A O C ^ = C O M ^ = 30 ° . (1)
Tia OC nằm giữa hai tia OA, OM nên từ (1) suy ra tia OC là tia phân giác của góc AOM.
b) Ta có O M ⊥ O N ⇒ M O N ^ = 90 ° .
Tia OA nằm giữa hai tia ON, OM nên A O N ^ + A O M ^ = M O N ^ .
Suy ra A O N ^ = M O N ^ − A O M ^ = 90 ° − 60 ° = 30 ° .
Vậy A O N ^ = A O C ^ = 30 ° (2)
Tia OA nằm giữa hai tia ON, OC nên từ (2) suy ra tia OA là tia phân giác của góc CON.

Vì OA' là tia đối của tia OA (gt)
OB' là tia đối của tia OB (gt)
⇒ ∠AOB = ∠A'OB'
Mà OM là tịa phân giác ∠AOB (gt)
⇒ ∠AOM = ∠AOB/2
Vì ON là tia phân giác của ∠A'OB' (gt)
⇒ A' A'OB' / 2
Mà ∠AOB = ∠A'OB' (cmt)
⇒ ∠AOB /2= ∠A'OB'/2
⇒ ∠AOM = ∠A'ON

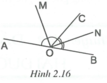
Ta có O M ⊥ O N ⇒ M O N ^ = 90 ° .
Tia OM là tia phân giác của góc AOC nên A O M ^ = M O C ^ .
Tia ON là tia phân giác của góc BOC nên B O N ^ = N O C ^ .
Xét tổng
A O C ^ + B O C ^ = 2 M O C ^ + 2 N O C ^ = 2 M O C ^ + N O C ^ = 2 M O N ^ = 2.90 ° = 180 ° .
Hai góc kề AOC và BOC có tổng bằng nên hai tia OA, OB đối nhau.
Đường trung trực – Hai góc có cạnh tương ứng vuông góc

CC' cắt BB'=>BOC=B'OC'
AA' cắt CC'=>AOC=A'OC'
OA và OA' là 2 tia nằm trên 2 nửa mặt phẳng bờ CC'
=>OA' và OB nằm trên cùng 1 nửa mặt phẳng bờ CC'
OB và OB' là 2 tia nằm trên 2 nửa mặt phẳng bờ CC'
=>OA' và OB' nằm trên 2 nửa mặt phẳng bờ CC'
=>OA' và OB' nằm trên 2 nửa mặt phẳng bờ OC'
=>OC' nằm giữa OA' và OB'
mà A'OC'=C'OB'=>OC' là tia phân giác của A'OB'
=>đpcm

a) Vì Oa⊥Ox⇒xOa=90o;Ob⊥Oy⇒yOb=90oOa⊥Ox⇒xOa=90o;Ob⊥Oy⇒yOb=90o
Ta có: xOa + aOy = xOy
=> 90o + aOy = xOy (1)
Lại có: xOb + bOy = xOy
=> xOb + 90o = xOy (2)
Từ (1) và (2) => aOy = xOb
b) Vì Om là phân giác của aOb nên bOm=mOa=aOb2bOm=mOa=aOb2
Lại có: aOy = xOb (theo câu a)
=> aOy + mOa = bOm + xOb
=> mOy = xOm
=> Om là tia phân giác của aOb (đpcm)

* Tìm cách giải
Muốn chứng tỏ tia OK là tia phân giác của góc AOB ta cần chứng tỏ A O K ^ = B O K ^ . Muốn vậy cần chứng tỏ A O N ^ + N O K ^ = B O M ^ + M O K ^ .
* Trình bày lời giải
Ta có O M ⊥ O A ⇒ A O M ^ = 90 ° ; O N ⊥ O B ⇒ B O N ^ = 90 ° .
Tia ON nằm giữa hai tia OA, OM nên A O N ^ + N O M ^ = A O M ^ = 90 ° ;
Tia OM nằm giữa hai tia OB, ON nên B O M ^ + M O N ^ = B O N ^ = 90 ° .
Suy ra A O N ^ = B O M ^ (cùng phụ với M O N ^ ).
Tia OK là tia phân giác của góc MON nên N O K ^ = M O K ^ .
Do đó A O N ^ + N O K ^ = B O M ^ + M O K ^ .(1)
Vì tia ON nằm giữa hai tia OA, OK và tia OM nằm giữa hai tia OB, OK nên từ (1) suy ra A O K ^ = B O K ^ . Mặt khác, tia OK nằm giữa hai tia OA, OB nên tia OK cũng là tia phân giác của góc AOB