Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Chọn B.
Ta có (II) đúng vì hàm số lượng giác liên tục trên từng khoảng của tập xác định.
Ta có (III) đúng vì 
Khi đó 
Vậy hàm số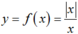 
liên tục tại x = 1.
Chọn C.
Với 
ta có hàm số 
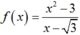liên tục trên khoảng 
và 
, (1).
Với 
ta có 
và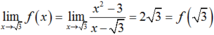 
nên hàm số liên tục tại 
, (2)
Từ (1) và (2) ta có hàm số liên tục trên R.
Chọn D.
Ta có (I) đúng vì f(x) = x5 – x2 + 1 là hàm đa thức nên liên tục trên R..
Ta có (III) đúng vì 
liên tục trên (2; +∞) và 
nên hàm số liên tục trên [2; +∞)
(!!) sai vì hàm số gián đoạn tại các điểm hàm số không xác định.
- Ta có (II) đúng vì hàm số lượng giác liên tục trên từng khoảng của tập xác định.
- Ta có (III) đúng vì
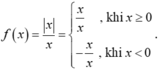
- Khi đó:
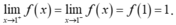
- Vậy hàm số
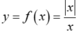
liên tục tại x = 1.
- (I) Sai vì với x < -1 thì hàm số đã cho không xác định nên tại các điểm x 0 < - 1 thì hàm số đã cho không liên tục.
Chọn D.
Chọn B.
Dễ thấy (I) sai ( với x không thuộc tập xác định thì tại điểm đó hàm số gián đoạn)
Khẳng định (II) là lí thuyết.
Hàm số: 
liên tục trên khoảng (-3; 3). Liên tục phải tại 3 và liên tục trái tại -3.
Nên 
liên tục trên đoạn [-3; 3].
Chọn B.
Ta có: D = (-∞; -2] ∪ [2; +∞).
.và f(2) = 0.
Vậy hàm số liên tục tại x = 2.
Với -2 < x < 2 thì hàm số không xác định.
+) Ta có (I) đúng vì f ( x ) = x 5 - x 2 + 1 là hàm đa thức nên liên tục trên R
+) Ta có (III) đúng vì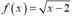 
liên tục trên (2;+∞) và 
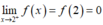nên hàm số liên tục trên [2;+∞).
+) (II) sai vì trên khoảng ( -1, 1)hàm số đã cho không xác định nên hàm số không liên tục trên khoảng đó.
Chọn D
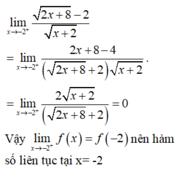
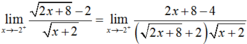
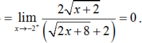
Mình nghĩ là tìm khẳng định sai chứ, vì b,c,d đều đúng
\(DKXD:x\ne\sqrt[3]{4}\approx1,58\in\left(-2;2\right)\)
Vậy thì hàm sẽ gián đoạn trên khoảng \(\left(-2;2\right)\) => đáp án A sai, còn lại tất cả đều đúng