Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Làm xuôi thì đơn giản, tính \(F'\left(x\right)\) là xong (chịu khó biến đổi)
Làm ngược thì nhìn biểu thức hơi thiếu thân thiện
\(\int\dfrac{2\sqrt{2}\left(x^2-1\right)}{x^4+1}dx=\int\dfrac{2\sqrt{2}\left(x^2-1\right)}{\left(x^2-x\sqrt{2}+1\right)\left(x^2+x\sqrt{2}+1\right)}dx\)
Phân tách hệ số bất định:
\(\dfrac{2\sqrt{2}\left(x^2-1\right)}{\left(x^2-x\sqrt{2}+1\right)\left(x^2+x\sqrt{2}+1\right)}=\dfrac{a\left(2x-\sqrt{2}\right)}{x^2-x\sqrt{2}+1}+\dfrac{b\left(2x+\sqrt{2}\right)}{x^2+x\sqrt{2}+1}\)
Quan tâm tử số: \(a\left(2x-\sqrt{2}\right)\left(x^2+x\sqrt{2}+1\right)+b\left(2x+\sqrt{2}\right)\left(x^2-x\sqrt{2}+1\right)\)
\(=2\left(a+b\right)x^3+\sqrt{2}\left(a-b\right)x^2+\sqrt{2}\left(b-a\right)\)
Đồng nhất 2 tử số: \(\left\{{}\begin{matrix}a+b=0\\a-b=2\\\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}a=1\\b=-1\end{matrix}\right.\)
Do đó:
\(\dfrac{2\sqrt{2}\left(x^2-1\right)}{x^4+1}=\dfrac{2x-\sqrt{2}}{x^2-x\sqrt{2}+1}-\dfrac{2x+\sqrt{2}}{x^2+x\sqrt{2}+1}\)
Cái tìm hệ số bất định ấy ạ, tại sao lại tách về 2x- căn 2 vậy anh?

Ý bạn là \(f(x)=\frac{1}{9+x^2}+\frac{3}{9+x^2}\) hay thế nào? Bạn cần viết đề bằng công thức toán (biểu tượng $\sum$ góc trái khung soạn thảo để được hỗ trợ tốt hơn).
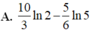
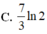
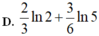


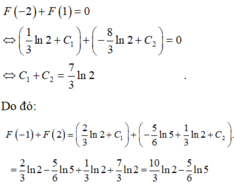
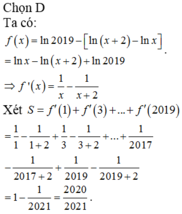
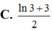
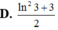

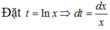
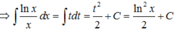
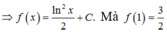
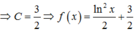
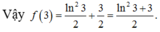
Chọn A