K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NV
Nguyễn Việt Lâm
Giáo viên
16 tháng 4 2021
17.
\(f\left(x\right)>0;\forall x\)
\(\Leftrightarrow\left\{{}\begin{matrix}a=1>0\left(luôn-đúng\right)\\\Delta'=\left(2m-1\right)^2-\left(3m^2-2m+4\right)< 0\end{matrix}\right.\)
\(\Leftrightarrow m^2-2m-3< 0\)
\(\Leftrightarrow-1< m< 3\)
\(\Rightarrow m=\left\{0;1;2\right\}\)
18.
\(\pi< x< \dfrac{3\pi}{2}\Rightarrow cosx< 0\)
\(\Rightarrow cosx=-\sqrt{1-sin^2x}=-\dfrac{\sqrt{5}}{3}\)
\(\Rightarrow tanx=\dfrac{sinx}{cosx}=\dfrac{2\sqrt{5}}{5}\)
\(tan\left(x+\dfrac{\pi}{4}\right)=\dfrac{tanx+tan\dfrac{\pi}{4}}{1-tanx.tan\dfrac{\pi}{4}}=\dfrac{\dfrac{2\sqrt{5}}{5}+1}{1-\dfrac{2\sqrt{5}}{5}.1}=9+4\sqrt{5}\)
NV
Nguyễn Việt Lâm
Giáo viên
16 tháng 4 2021
19.
\(a^2=b^2+c^2+bc\Rightarrow b^2+c^2-a^2=-bc\)
\(\Rightarrow cosA=\dfrac{b^2+c^2-a^2}{2bc}=\dfrac{-bc}{2bc}=-\dfrac{1}{2}\)
\(\Rightarrow A=120^0\)
20.
Đường tròn (C) tâm \(I\left(2;-1\right)\) bán kính \(R=2\)
\(d\left(I;\Delta\right)=\dfrac{\left|2-1-3\right|}{\sqrt{1^2+1^2}}=\sqrt{2}\)
Gọi H là trung điểm AB \(\Rightarrow\left\{{}\begin{matrix}IH=d\left(I;\Delta\right)\\AH=\dfrac{1}{2}AB\end{matrix}\right.\)
Áp dụng định lý Pitago trong tam giác vuông IAH:
\(IA^2=IH^2+AH^2\Leftrightarrow R^2=IH^2+AH^2\)
\(\Rightarrow AH=\sqrt{2}\Rightarrow AB=2AH=2\sqrt{2}\)
cho em hỏi là 84 = mấy mũ 2 vậy ạ
AH
Akai Haruma
Giáo viên
12 tháng 1 2023
y' là đạo hàm bậc nhất của y. Bạn đọc sách toán phổ thông phần đạo hàm/ tìm max min của hàm số hoặc google search để tìm hiểu rõ hơn.
BN
2
BT
1
HA
13 tháng 6 2016
\(ĐKXĐ:sinx\ne0\\ \Leftrightarrow x\ne k\pi\left(k\in Z\right)\\ 1-cot^4x=\frac{2}{sin^2x}-\frac{1}{sin^4x}\\ \Leftrightarrow\left(1-cot^2x\right)\left(1+cot^2x\right)=\frac{1}{sin^2x}\left(2-\frac{1}{sin^2x}\right)\)
\(\Leftrightarrow\left(2-1-cot^2x\right).\frac{1}{sin^2x}=\frac{1}{sin^2x}\left(2-\frac{1}{sin^2x}\right)\\ \Leftrightarrow2-\frac{1}{sin^2x}=2-\frac{1}{sin^2x}\)
=> điểu phải chứng minh
NV
Nguyễn Việt Lâm
Giáo viên
23 tháng 3 2022
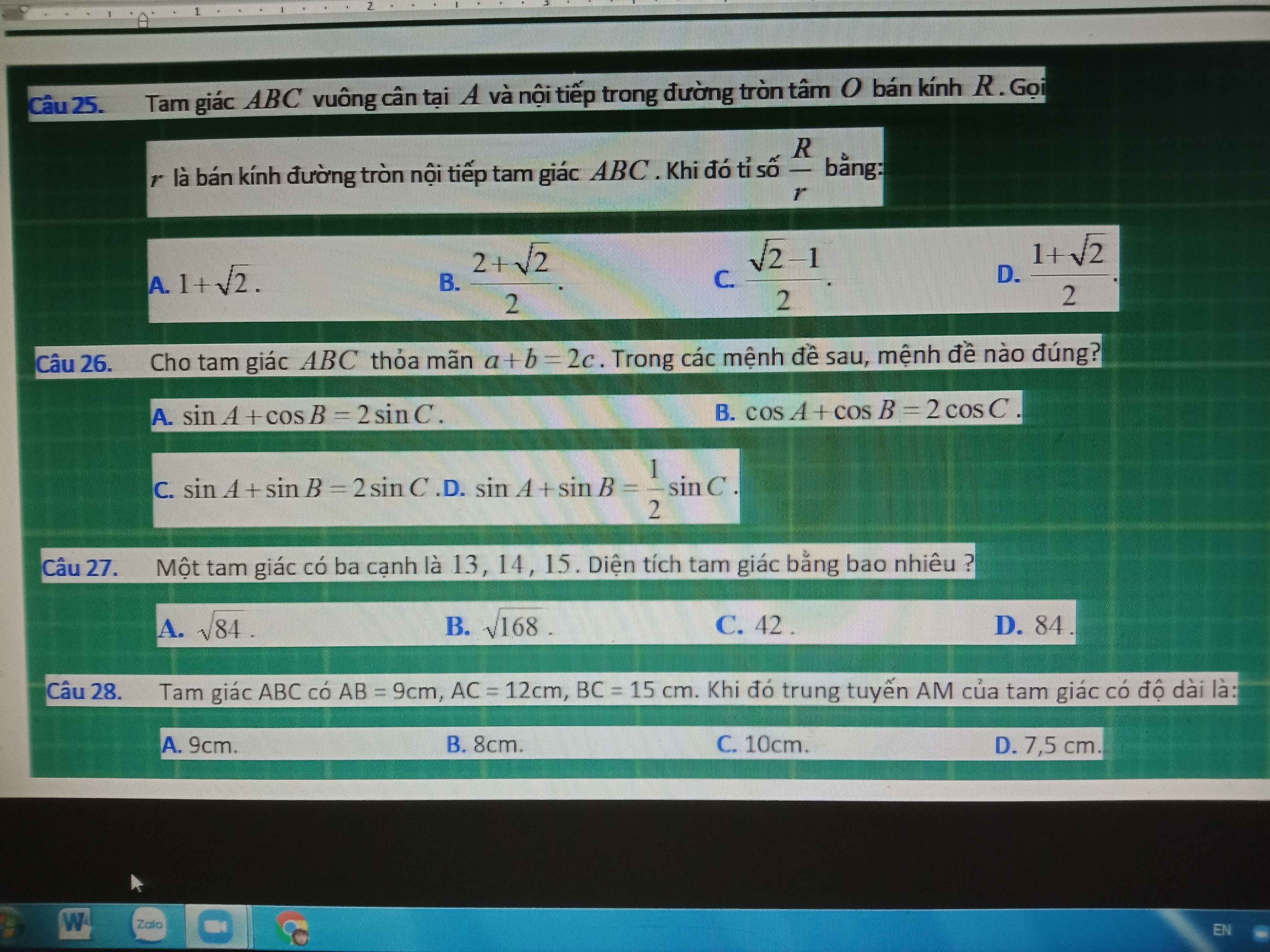
25.
\(R=\dfrac{BC}{2}\)
\(r=\dfrac{BC}{2}.tan\left(\dfrac{45^0}{2}\right)=\dfrac{BC\left(\sqrt{2}-1\right)}{2}\)
\(\Rightarrow\dfrac{R}{r}=\dfrac{1}{\sqrt{2}-1}=1+\sqrt{2}\)
26.
\(\left\{{}\begin{matrix}a=2R.sinA\\b=2RsinB\\c=2RsinC\end{matrix}\right.\) \(\Rightarrow2R.sinA+2R.sinB=2.2R.sinC\)
\(\Rightarrow sinA+sinB=2sinC\)
27.
\(p=\dfrac{13+14+15}{2}=21\)
\(S=\sqrt{p\left(p-13\right)\left(p-14\right)\left(p-15\right)}=84\)
28.
\(AM=\sqrt{\dfrac{2\left(AB^2+AC^2\right)-BC^2}{4}}=7,5\left(cm\right)\)
16 tháng 4 2020
| x + 3 | - 6x + 1 = | x + 1 |
<=> | x + 3 | - | x + 1 | - 6x + 1 = 0
Phương trình này em xét dấu và kẻ bảng rồi chia trường hợp:
ukm