Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

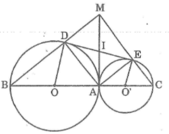
Tứ giác ADME là hình chữ nhật và ID = IE (chứng minh trên) nên đường chéo AM của hình chữ nhật phải đi qua trung điểm I của DE. Suy ra: A, I, M thẳng hàng.
Ta có: IA ⊥ OO’ (vì IA là tiếp tuyến của (O))
Suy ra: AM ⊥ OO’
Vậy MA là tiếp tuyến chung của đường tròn (O) và (O’)

a) vuông, nên
Kc là tiếp tuyến, KEF là cát tuyến nên
Suy ra , nên
Ta có nên , từ đó EMOF là tứ giác nội tiếp. (1)
b) Đặt . Ta có ... )uôn nên là ến, KFàcáê u êT c\(DeltaKM\simDetaF.g êtđó O àt gánội ế 1)ặ aó ,nên là tứ iá ộ tip. (2ừ (1) ()y ramđi A , F tộc cng một đường đườgính ủ


a) Hai tam giác vuông ABO và ACO có chung cạnh huyền AO nên A, B, O, C cùng thuộc đường tròn đường kính AO.
Vậy tứ giác ABOC là tứ giác nội tiếp.
b) Ta thấy ngay \(\Delta ABD\sim\Delta AEB\left(g-g\right)\)
\(\Rightarrow\frac{AB}{AE}=\frac{AD}{AB}\Rightarrow AE.AD=AB^2\)
Xét tam giác vuông ABO có BH là đường cao nên áp dụng hệ thức lượng ta có:
\(AH.AO=AB^2\)
Suy ra AD.AE = AH.AO
c) Ta có \(\widehat{PIK}+\widehat{IKQ}+\widehat{P}+\widehat{Q}=360^o\)
\(\Rightarrow2\left(\widehat{PIO}+\widehat{P}+\widehat{OKQ}\right)=360^o\)
\(\Rightarrow\widehat{PIO}+\widehat{P}+\widehat{OKQ}=180^o\)
Mặt khác \(\widehat{PIO}+\widehat{P}+\widehat{IOP}=180^o\)
\(\Rightarrow\widehat{IOP}=\widehat{OKQ}\Rightarrow\Delta PIO\sim\Delta QOK\)
\(\Rightarrow\frac{IP}{PO}=\frac{OQ}{KQ}\Rightarrow PI.KQ=PO^2\)
Sử dụng bất đẳng thức Cô-si ta có:
\(IP+KQ\ge2\sqrt{IP.KQ}=2\sqrt{OP^2}=PQ\)
acje cho hỏi 2 tam giác đồng dạng ở câu b là góc nào í chỉ ro rõ cho e với ạk