Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: góc AKB=1/2*sđ cung AB=90 độ
góc HCB+góc HKB=180 độ
=>HCBK nội tiếp
b: Xét ΔACH vuông tại C và ΔAKB vuông tại K có
góc CAH chung
=>ΔACH đồng dạng với ΔAKB
=>AC/AK=AH/AB
=>AK*AH=AB*AC=2R*1/2R=R^2

a: góc AKB=1/2*180=90 độ
góc HCB+góc HKB=180 độ
=>BKHC nội tiếp
b: Xét ΔACH vuông tại C và ΔAKB vuông tại K có
góc CAH chug
=>ΔACH đồng dạng với ΔAKB
=>AC/AK=AH/AB
=>AK*AH=AC*AB=1/2R*2R=R^2

Ta có: góc AKP = 90độ ( Góc nội tiếp chắn nửa đường tròn)
Mà AK giao MN tại H =) Góc HKP = 90độ (1)
Lại có: MC vuông góc AB =) Góc HCB = 90độ (2)
Từ (1) và (2) =) góc HKP + góc HCP = 180độ
Mà 2 góc đối nhau
=) Tứ giác BCHK nội tiếp

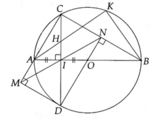
a, H I B ^ = H K B ^ = 180 0
=> Tứ giác BIHK nội tiếp
b, Chứng minh được: DAHI ~ DABK (g.g)
=> AH.AK = AI.AB = R 2 (không đổi)
c, Chứng minh được MCND là hình chữ nhật từ đó => Đpcm

a: Xét (O) có
ΔAKB nội tiếp
AB là đường kính
=>ΔAKB vuông tại K
Xét tứ giác BKHI có
góc BKH+góc BIH=180 độ
=>BKHI là tứ giác nội tiếp
b: Xét ΔAHI vuông tại I và ΔABK vuông tại K có
góc HAI chung
=>ΔAHI đồng dạng với ΔABK
=>AH/AB=AI/AK
=>AH*AK=AI*AB=1/4*R^2


1) Xét (O) có
ΔKAB nội tiếp đường tròn(K,A,B\(\in\)(O))
AB là đường kính
Do đó: ΔKAB vuông tại K(Định lí)
\(\Leftrightarrow\widehat{AKB}=90^0\)
hay \(\widehat{HKB}=90^0\)
Xét tứ giác BKHC có
\(\widehat{HKB}\) và \(\widehat{HCB}\) là hai góc đối
\(\widehat{HKB}+\widehat{HCB}=180^0\left(90^0+90^0=180^0\right)\)
Do đó: BKHC là tứ giác nội tiếp(Dấu hiệu nhận biết tứ giác nội tiếp)
hay B,K,H,C cùng thuộc một đường tròn(đpcm)