Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a) ta có : AN = AM (tính chất tiếp tuyến)
\(\Rightarrow\) tam giác AMN cân tại A
OA là tia phân giác cũng là đường cao
\(\Rightarrow\) OA \(\perp\) MN (đpcm)
b) đặc H là giao điểm của MN và AO
ta có MH = HN (OA \(\perp\) MN \(\Rightarrow\) H là trung điểm MN)
mà CO = CN = R
\(\Rightarrow\) OH là đường trung bình của tam giác MNC
\(\Rightarrow\) OH // MC \(\Leftrightarrow\) MC // OA (đpcm)
format('truetype')%3Bfont-weight%3Anormal%3Bfont-style%3Anormal%3B%7D%3C%2Fstyle%3E%3C%2Fdefs%3E%3Ctext%20font-family%3D%22math11ce3e6e3f452828e23a0c94572%22%20font-size%3D%2216%22%20text-anchor%3D%22middle%22%20x%3D%228.5%22%20y%3D%2216%22%3E%26%23x22A5%3B%3C%2Ftext%3E%3C%2Fsvg%3E)
MN
b) Vẽ đường kính NOC. Chứng minh: MC // AO
c) Tính chu vi format('truetype')%3Bfont-weight%3Anormal%3Bfont-style%3Anormal%3B%7D%3C%2Fstyle%3E%3C%2Fdefs%3E%3Ctext%20font-family%3D%22math1ed582716bfb4738ccd92405301%22%20font-size%3D%2216%22%20text-anchor%3D%22middle%22%20x%3D%227.5%22%20y%3D%2216%22%3E%26%23x2206%3B%3C%2Ftext%3E%3C%2Fsvg%3E)
AMN biết OM= 3cm và OA = 5cm
a) Xét (O) có
AM là tiếp tuyến có M là tiếp điểm(gt)
AN là tiếp tuyến có N là tiếp điểm(gt)
Do đó: AM=AN; OM=ON(Tính chất hai tiếp tuyến cắt nhau)
Ta có: AM=AN(cmt)
nên A nằm trên đường trung trực của MN(Tính chất đường trung trực của một đoạn thẳng)(1)
Ta có: OM=ON(cmt)
nên O nằm trên đường trung trực của MN(Tính chất đường trung trực của một đoạn thẳng)(2)
Từ (1) và (2) suy ra AO là đường trung trực của MN
hay AO⊥MN(đpcm)
b) Xét (O) có
ΔMNC nội tiếp đường tròn(C,M,N∈(O))
NC là đường kính
Do đó: ΔMNC vuông tại M(Định lí)
⇒MN⊥MC
Ta có: MN⊥MC(cmt)
MN⊥AO(cmt)
Do đó: MC//AO(Định lí 1 từ vuông góc tới song song)
c) Áp dụng định lí Pytago vào ΔOMA vuông tại M, ta được:
\(OA^2=OM^2+MA^2\)
\(\Leftrightarrow AM^2=OA^2-OM^2=5^2-3^2=16\)
hay \(AM=\sqrt{16}=4cm\)
mà AM=AN(cmt)
nên AN=4cm
Gọi H là giao điểm của MN và AO
mà MN⊥AO tại trung điểm của MN
nên H là trung điểm của MN và MH⊥AO tại H
Áp dụng hệ thức lượng trong tam giác vuông vào ΔAMO vuông tại M, ta được:
\(MH\cdot AO=MO\cdot MA\)
\(\Leftrightarrow MH\cdot5=4\cdot3=12\)
hay MH=2,4cm
mà \(MN=2\cdot MH\)(H là trung điểm chung của MN)
nên \(MN=2\cdot2.4=4.8cm\)
Chu vi tam giác AMN là:
\(C=AM+AN+MN=5+5+4.8=14.8cm\)
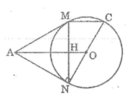
Ta có: AN ⊥ NC (tính chất tiếp tuyến)
Áp dụng định lí Pitago vào tam giác vuông AON ta có :
A O 2 = A N 2 + O N 2
Suy ra : A N 2 = A O 2 - O N 2 = 5 2 - 3 2 = 16
AN = 4 (cm)
Suy ra: AM = AN = 4 (cm)
Gọi H là giao điểm của AO và MN
Ta có: MH = NH = MN/2 (tính chất tam giác cân)
Tam giác AON vuông tại N có NH ⊥ AO. Theo hệ thức lượng trong tam giác vuông, ta có:
OA.NH = AN.ON ⇒ NH = (AN.ON)/AO = (4.3)/5 = 2,4 (cm)
MN = 2.NH = 2.2,4 = 4,8 (cm)
a,theo t/c 2 tiếp tuyến cắt nhau thì \(MA=NA\Rightarrow\Delta AMN\) cân và \(OA\) la p/g cua goc MAN \(\Rightarrow AO\) là dg p/g đóng vai vai trò đg cao \(\Rightarrow AO\perp MN\)
b,tam giác CMN có CN là đg kính nên tam giác CMN là tam giác vuông nên goc CMO +goc OMN =90 mat khác góc OMN+góc AOM =90 (MN \(\perp\) OA)\(\Rightarrow\)góc CMO =goc AOM(cùng phụ góc OMN) ở vị trí so le trong nên MC song song voi AO
C,xet \(\Delta OMA\) có \(AM=\sqrt{OA^2-OM^2}=\sqrt{5^2-3^2}=4\Rightarrow AN=AM=4\)
va MH=\(\frac{MA.MO}{OA}=\frac{4.3}{5}=2.4\Rightarrow MN=2MH=4.8\)
mình làm có gì sai mong bạn bỏ qua
a) Ta có : OM = ON ( =R )
=> O thuộc trung trực của MN (1)
AM = AN ( tính chất 2 tt cắt nhau )
=> A thuộc trung trực của MN (2)
Từ (1) và (2) => OA là đường trung trực của đoạn thẳng MN
Vậy : \(OA\perp MN\left(đpcm\right)\)
b) Xét tam giác MNC , ta có : MO = NO = OC ( =bk )
\(\Rightarrow MO=\frac{1}{2}NC\Rightarrow\Delta MNC\)vuông tại M
\(\Rightarrow MC\perp MN\left(3\right)\)
Theo ( c/m câu a ) : \(OA\perp MN\left(4\right)\)
Từ (3) và (4) => MC // AO ( đpcm )
c) Áp dụng đlí Py -ta - go cho tam giác AMO vuông tại M , ta có :
\(OA^2=AM^2+MO^2\)
\(AM^2=OA^2-MO^2=5^2-3^2=16\)
\(AM^2=16\Rightarrow AM=4\left(cm\right)\)
Áp dụng hệ thức lượng cho tam giác AMO vuông tại M , đường cao MI :
Ta có : AM . MO = AO . MI
\(MI=\frac{AM.MO}{AO}=\frac{4.3}{5}=2,4\)
\(\Rightarrow MN=2.MI=2.2,4=4,8\)
Vậy : AM = AN = 4cm
MN = 4,8 cm
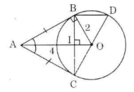
a) Ta có: AB = AC (tính chất của hai tiếp tuyến cắt nhau). Nên ΔABC cân tại A.
Lại có AO là tia phân giác của góc A nên AO ⊥ BC. (trong tam giác cân, đường phân giác cũng là đường cao)
b) Gọi I là giao điểm của AO và BC. Suy ra BI = IC (đường kính vuông góc với một dây).
Xét ΔCBD có :
CI = IB
CO = OD (bán kính)
⇒ BD // HO (HO là đường trung bình của BCD) ⇒ BD // AO.
c) Theo định lí Pitago trong tam giác vuông OAC:
A C 2 = O A 2 – O C 2 = 4 2 – 2 2 = 12
=> AC = √12 = 2√3 (cm)
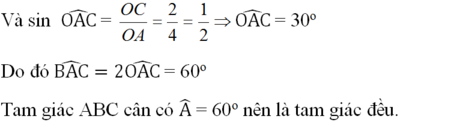
Do đó AB = BC = AC = 2√3 (cm).
Cho sửa lại đề tí ==* , câu b) là c/m MR // AO => MC // AO :>
a. Ta có: AM = AN (tính chất hai tiếp tuyến cắt nhau)
Suy ra tam giác AMN cân tại A
Mặt khác AO là đường phân giác của góc MAN ( tính chất hai tiếp tuyến cắt nhau )
Suy ra AO là đường cao của tam giác AMN ( tính chất tam giác cân )
Vậy \(OA\perp MN\)
b. Tam giác MNC nội tiếp trong đường tròn (O) có NC là đường kính nên góc (CMN) = 90o
Suy ra: \(NM\perp MC\)
Mà \(OA\perp MN\)(chứng minh trên)
Suy ra: OA // MC
c. Ta có: \(AN\perp NC\) (tính chất tiếp tuyến)
Áp dụng định lí Pitago vào tam giác vuông AON ta có :
AO2 = AN2 + ON2
Suy ra : AN2 = AO2 – ON2 = 52 – 32 = 16
AN = 4 (cm)
Suy ra: AM = AN = 4 (cm)
Gọi H là giao điểm của AO và MN
Ta có: \(MH=NH=\frac{MN}{2}\) (tính chất tam giác cân)
Tam giác AON vuông tại N có \(NH\perp AO\). Theo hệ thức lượng trong tam giác vuông, ta có:
OA . NH = AN . ON => \(NH=\frac{\left(AN.ON\right)}{AO}=\frac{\left(4.3\right)}{5}=2,4\)
MN = 2.NH = 2.2,4 = 4,8 (cm)
Vậy .....................