Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a, HS tự chứng minh
b, OM = R 2
c, MC. MD = M A 2 = MH.MO
=> MC. MD = MH.MO
=> DMHC ~ DMDO (c.g.c)
=> M H C ^ = M D O ^ => Tứ giác CHOD nội tiếp
Chứng minh được: M H C ^ = O H D ^
=> C H B ^ = B H D ^ (cùng phụ hai góc bằng nhau)

1) Hình vẽ câu 1) đúng
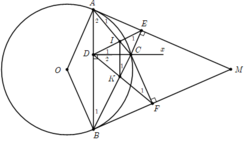
Ta có A E C ^ = A D C ^ = 90 0 ⇒ A E C ^ + A D C ^ = 180 0 do đó, tứ giác ADCE nội tiếp.
2) Chứng minh tương tự tứ giác BDCF nội tiếp.
Do các tứ giác A D C E , B D C F nội tiếp nên B 1 ^ = F 1 ^ , A 1 ^ = D 1 ^
Mà AM là tiếp tuyến của đường tròn (O) nên A 1 ^ = 1 2 s đ A C ⏜ = B 1 ^ ⇒ D 1 ^ = F 1 ^ .
Chứng minh tương tự E 1 ^ = D 2 ^ . Do đó, Δ C D E ∽ Δ C F D g.g
3) Gọi Cx là tia đối của tia CD
Do các tứ giác A D C E , B D C F nội tiếp nên D A E ^ = E C x ^ , D B F ^ = F C x ^
Mà M A B ^ = M B A ^ ⇒ E C x ^ = F C x ^ nên Cx là phân giác góc E C F ^ .
4) Theo chứng minh trên A 2 ^ = D 2 ^ , B 1 ^ = D 1 ^
Mà A 2 ^ + B 1 ^ + A C B ^ = 180 0 ⇒ D 2 ^ + D 1 ^ + A C B ^ = 180 0 ⇒ I C K ^ + I D K ^ = 180 0
Do đó, tứ giác CIKD nội tiếp ⇒ K 1 ^ = D 1 ^ mà D 1 ^ = B 1 ^ ⇒ I K / / A B

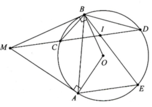
a, Vì M B C ^ = M D B ^ = 1 2 s đ C B ⏜ nên chứng minh được ∆MBC:∆MDB (g.g)
b, Vì
M
B
O
^
+
M
A
O
^
=
180
0
nên tứ giác MAOB nội tiếp
c, Đường tròn đường kính OM là đường tròn ngoại tiếp tứ giác MAOB => r = M O 2
Gọi H là giao điểm của AB với OM
=> OH ⊥ AB; AH = BH = R 3 2
Giải tam giác vuông OAM, đường cao AH ta được OM = 2R Þ r = R
d, Ta có M I B ^ = s đ D E ⏜ + s đ B C ⏜ 2 và M A B ^ = s đ A C ⏜ + s đ B C ⏜ 2
Vì AE song song CD => s đ D E ⏜ = s đ A C ⏜ => M I B ^ = M A B ^
Do tứ giác MAIB nội tiếp hay 5 điểm A, B, O, I, M nằm trên cùng 1 đường tròn kính MO
Từ đó ta có được M I O ^ = 90 0 => OI ⊥ CD hay I là trung điểm của CD